In the previous section 4.31, we completed the discussion on Valence bond theory. In this section, we will see Molecular orbital theory
• Consider the hybridization concept that we saw in the previous sections
• We saw that:
♦ When two atoms combine to form molecules, new orbitals are formed in the central atom
✰ These new orbitals are called hybrid orbitals
♦ The orbitals of the 'outer atoms' overlap with the newly formed hybrid orbitals of the 'central atom'
♦ Thus new molecules are formed
• In our present case of molecular bond theory also, new orbitals are formed
✰ These new orbitals are called molecular orbitals
• There is a major difference between ‘hybrid orbitals’ and ‘molecular orbitals’. It can be explained in 3 steps:
1. The hybrid orbitals have a single center point
♦ The nucleus of the central atom is that center point
2. But the molecular orbitals have more than one center points
♦ The nuclei of the combining atoms are those center points
3. So we can write:
• A hybrid orbital has only one owner
♦ The owner is the central atom
• A molecular orbital has more than one owners
♦ The owners are the atoms which combine to form that molecule
• We will first see the formation of the simplest molecular orbitals. It can be written in 8 steps:
1. Consider the 1s orbital of a H atom
♦ We will call this H atom as: HA
2. It is going to interact with the 1s orbital of another H atom
♦ We will call this H atom as: HB
3. So the two spheres comes closer and closer to each other
• What will happen when they interact?
• The following steps from (4) to () will give the answer:
4. To find the answer,
• We must first accept the ‘fundamental fact’: electrons behave as waves
• We must also accept the fact that, they are 3D waves
♦ That means the 'wave associated with an electron' occupies a three dimensional space
♦ The wave is not confined to a line (1D)
♦ The wave is not confined to a plane (2D)
5. But for simplicity, we will draw them as 2D waves in our present discussion
• Fig.4.184(a) below shows
♦ The wave associated with the electron in HA atom
♦ The wave associated with the electron in HB atom
6. Let us add the two waves
• There are two types of addition
♦ When two waves are added, both 'types of addition' will take place
♦ We cannot choose one and stop the other from taking place
Type 1:
This can be explained in 4 steps:
(i) In fig.4.184(a), the crests of HA are in line with the crests of HB
♦ This is indicated by the red dotted lines
(ii) So naturally, the troughs will also be in line
(iii) When the two waves add, we get a single ‘new wave’
♦ This ‘new wave’ will be in favor of 'keeping the two H electrons together'
♦ So this ‘new wave’ will be in favor of ‘H2 bond formation’
(iv) We say that: this addition is constructive
Type 2:
This can be explained in 4 steps:
(i) In fig.4.184(b), the crests of HA are in line with the troughs of HB
♦ This is indicated by the green dotted lines
(ii) Here also, when the two waves add, we get a single ‘new wave’
♦ This ‘new wave’ will not be in favor of 'keeping the two H electrons together'
✰ This is because of the mismatch between crests and troughs
✰ They are ‘out of phase’
(iii) The two electrons will try to repel each other
♦ So this ‘new wave’ will not be in favor of ‘H2 bond formation’
(iv) We say that: this addition is destructive
7. When the two 1s spheres interact, they merge together.
• The 'results of the merger' can be written in 2 steps:
(i) Formation of new orbitals
• During merger, both constructive and destructive additions takes place
♦ The constructive addition gives rise to a new orbital called bonding orbital
♦ The destructive addition gives rise to a new orbital called anti-bonding orbital
■ The new orbitals thus formed are called molecular orbitals
(ii) Non-existence of old orbitals
• After the merger, the following two orbitals will no longer exist:
♦ The 1s orbital of HA
♦ The 1s orbital of HB
8. Let us see the actual shapes of the new molecular orbitals
It can be written in two steps (A) and (B):
A. Bonding orbital
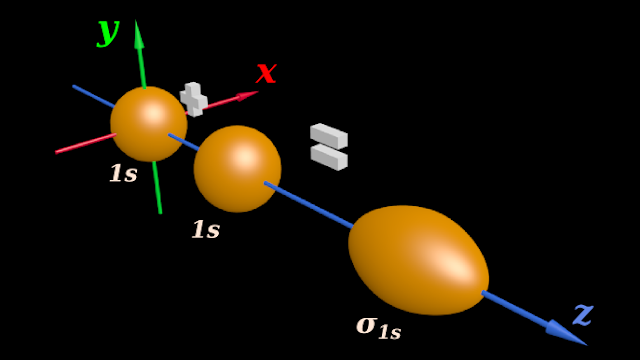
(i) The constructive addition resulting in the formation of bonding orbital is shown in fig.4.185 below:
♦ The 1s orbital at the origin of the coordinate axes belongs to the HA atom
♦ The other 1s orbital belongs to the HB atom
♦ (Note that, the z-axis is taken as the inter-nuclear axis)
(ii) The resulting molecular orbital has an oval shape
♦ We have to give it a suitable name
♦ We see that, the two 1s spheres add 'in a end-to-end manner' along the inter-nuclear axis
♦ So the resulting molecular orbital is denoted by the symbol 'σ'
♦ Recall the ‘formation of σ bonds’ in the topic of hybridization (See fig.4.142 of section 4.25)
(iii) In or present case, the molecular orbital is formed by the merger of two 1s orbitals
♦ So we call the resulting molecular orbital as: σ1s
(iv) The above fig.4.185 is a 3D view. Such a view helps us to understand the actual shapes
• But in the present case, a 2D view will give us some extra details. It is shown in fig.4.186 below:
• The orbitals are given a bit of transparency
✰ So the nuclei are also visible. They are denoted by small red spheres
(v) In fig.4.186, consider the shape of σ1s
♦ Consider the region between the two nuclei
✰ This region is thicker
✰ This thicker region is at the exact middle portion between the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thicker portion is at the exact middle portion)
(vi) That means, the electrons will be spending more time in the middle portion between the two nuclei
♦ So both the nuclei has a strong influence on the two electrons
♦ This gives rise to a strong bond between the two nuclei
♦ Thus a strong H-H bond is formed, resulting in the H2 molecule
B. Anti-bonding orbital
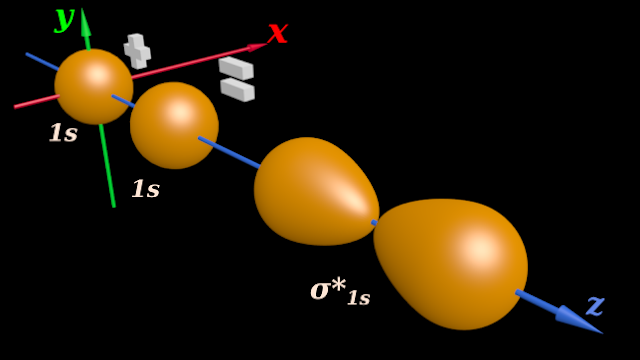
(i) The destructive addition resulting in the formation of anti-bonding orbital is shown in fig.4.187 below:
♦ The 1s orbital at the origin of the coordinate axes belongs to the HA atom
♦ The other 1s orbital belongs to the HB atom
♦ (Note that, the z-axis is taken as the inter-nuclear axis)
(ii) The resulting molecular orbital has two separate lobes
♦ We have to give it a suitable name
♦ We see that, the two 1s spheres add 'in a end-to-end manner' along the inter-nuclear axis
♦ So the resulting molecular orbital is denoted by the 'σ' symbol
♦ Recall the ‘formation of σ bonds’ in the topic of hybridization (See fig.4.142 of section 4.25)
(iii) In our present case, the molecular orbital is formed by the merger of two 1s orbitals
♦ But the resulting molecular orbital is an anti-bonding orbital
♦ We have to distinguish it from the bonding orbital. For that, we give an extra '*' symbol
♦ So we call the resulting anti-bonding molecular orbital as: σ*1s
(iv) The above fig.4.186 is a 3D view. Such a view helps us to understand the actual shapes
• But in the present case, a 2D view will give us some extra details. It is shown in fig.4.188 below:
• The orbitals are given a bit of transparency
✰ So the nuclei are also visible. They are denoted by small red spheres
(v) In fig.4.188, consider the shape of σ*1s
♦ Consider the region between the two nuclei
✰ This region is thinner
✰ This thinner region is at the exact middle portion between the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thinner portion is at the exact middle portion)
(vi) In fig.4.188, consider the shape of σ*1s
♦ Consider the regions on the left and right sides of the two nuclei
✰ Those regions are thicker
✰ Those thicker regions are symmetrically distributed on either sides of the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thicker portions are symmetrically distributed)
(vii) That means, the electrons will be spending more time away from the two nuclei
• It is clear that, in the σ*1s,
♦ The left side nucleus has no influence on the right side electron
♦ The right side nucleus has no effect on the left side electron
• The two 1s orbitals were independent before bond formation
• Now, even after the formation of the anti-bond, they are trying to separate away from each other
• This is because of the repulsion between the two nuclei
(viii) In fact, there is a definite plane between the two nuclei in the σ*1s
• This plane can be clearly marked in the 3D view. This is shown in the fig.4.189 below:
• In this plane, we will never find any electrons. It is a nodal plane
■ So it is clear that, anti-bonding will not help in the formation of H-H bond
(Note that in the 2D view, this plane will appear only as a very thin line. We will not be able to fully appreciate it's planar characteristics. So both 2D and 3D diagrams have advantages as well as disadvantages)
• There are more complex molecular orbitals to learn. We will see them in later sections
• Right now, we have to learn some more details about the H2 molecule
• Initially we had
♦ 1s orbital of HA
♦ 1s orbital of HB
• After bond formation, in the H2 molecule, we do not have the 1s orbitals
• In the H2 molecule, we have
♦ The molecular orbital σ1s
✰ This is a bonding orbital
♦ The molecular orbital σ*1s
✰ This is a anti-bonding orbital
■ We want to know how the two electrons in the H2 molecule is distributed among the two molecular orbitals
• For that, we use a graphical method. It can be explained in 6 steps:
1. In this graphical method, the energy increases as we go upwards
[Recall that, this usually is the case. The orbitals (square boxes with two opposite arrows inside) with higher energies are shown towards the top. The orbitals with lower energies are shown towards the bottom]
• Such a graphical representation is shown in fig.4.190 below:
2. The initial 1s orbitals are shown at the same horizontal level
• Because, they have the same energy
3. The sloping green lines indicate that:
♦ The two 1s orbitals combine together to form σ1s
✰ This σ1s is shown at a lower level than that of the 1s orbitals
4. The sloping magenta lines indicate that:
♦ The two 1s orbitals combine together to form σ*1s
✰ This σ*1s is shown at a higher level than that of the 1s orbitals
5. Why is σ1s shown at a lower level than 1s?
• The answer can be written in 4 steps
(i) Consider the Earth-stone system
• The energy of the system is due to the attraction between the earth and the stone
♦ When the stone is high up above the ground, the energy will be high (less negative)
♦ When the stone is near the ground, the energy will be low (more negative)
• This type of 'increase or decrease in energy' depends on 'distance between Earth and the stone'
(ii) The 'energy can increase or decrease' depending on the masses also
♦ If the mass of the earth decrease, the energy will increase (become less negative)
♦ If the mass of the earth increases, the energy will decrease (become more negative)
(iii) Let us now consider a system of two charges
• It is similar to the Earth-stone system
• The ‘type of energy change’ described in (ii) can occur in the case of a two-charge system also. But instead of mass, we consider 'magnitude of the charge'
♦ If one of the charges is decreased in magnitude, the attraction will decrease
✰ Consequently, the energy of the system will increase (become less negative)
♦ If one of the charges is increased in magnitude, the attraction will increase
✰ Consequently, the energy of the system will decrease (become more negative)
(iv) Now we compare the charges in the two types of orbitals: 1s and σ1s
♦ In the 1s orbitals, the ‘attraction on electrons’ is exerted by a single nucleus
♦ In the σ1s orbital, the ‘attraction on electrons’ is exerted by two nuclei. This attraction is greater
• So the energy of the σ1s will be lower than that of 1s
• That is why σ1s is shown at a lower level than 1s
(We will see a more detailed explanation when we learn about 'interactions between charged particles' in physics classes)
6. Why is σ*1s shown at a higher level?
• The answer can be written in 6 steps:
(i) In (5), we saw that:
♦ There is greater attraction in σ1s than in 1s
(ii) We also saw that:
♦ Greater attraction leads to lesser energy
(iii) So the opposite must be true:
♦ Lesser attraction leads to greater energy
(iv) We can decrease the attraction further:
♦ Further decrease in attraction leads to still greater energy
(v) Lesser and lesser attraction will finally become repulsion
♦ So repulsion will lead to very high energy
(vi) Now we compare the two types of orbitals: 1s and σ*1s
♦ In 1s, there is attraction
♦ In σ*1s, there is actually repulsion between the two lobes
• So σ*1s will have a higher energy than 1s
• That is why σ*1s is shown at a higher level than 1s
1. Initial state
• Initially, the two hydrogen atoms HA and HB are independent
♦ The electron of HA resides in the 1s orbital of HA
♦ The electron of HB resides in the 1s orbital of HB
2. Bonded state
• The two atoms bond together to form one H2 molecule
♦ For the bond formation, the two 1s orbitals merge together to give two new orbitals
✰ The bonding orbital σ1s
✰ The anti-bonding orbital σ*1s
• After the bond formation, the initial 1s orbitals will no longer exist
3. Energy levels
♦ The σ1s has a lower energy than 1s
♦ The σ*1s has a higher energy than 1s
• Then where will the two electrons reside?
• The answer can be written in steps:
1. Obviously, they have no where else to go but the σ1s and σ*1s
♦ The two electrons will go to those new molecular orbitals
2. They will be looking for the orbital with the ‘least energy level’
♦ We have seen that, compared to the anti-bonding orbital , the bonding orbital has lesser energy
♦ So the two electrons will approach σ1s
3. First, one of the two electrons enter the σ1s
• We know that an atomic orbital can hold a maximum of two electrons
♦ This applies to molecular orbitals also
♦ So the second electron can also enter the σ1s
4. So the square denoting σ1s will contain two opposite arrows
♦ This is shown in fig.4.190(b) above
♦ The square denoting σ*1s will be left vacant
1. Number of electrons occupying each orbital:
♦ Let Nb be the number of electrons occupying the bonding orbital σ1s
♦ Let Na be the number of electrons occupying the anti-bonding orbital σ*1s
2. If Nb > Na, we can write:
♦ The number of electrons trying to keep the two nuclei together is greater
♦ than
♦ The number of electrons trying to repel the two nuclei
■ This will result in a stable molecule
3. If Na > Nb, we can write:
♦ The number of electrons trying to repel the two nuclei is greater
♦ than
♦ The number of electrons trying to keep the two nuclei together
■ This will result in a unstable molecule
4. So in our present case of H2 molecule, we have:
♦ Nb = 2 and Na = 0
♦ So Nb > Na
■ Thus we can confirm that H2 is a stable molecule
• For that, we introduce a concept called bond order
• Bond order (b.o) can be defined in 3 steps:
1. Number of electrons occupying each orbital:
♦ Write the number (Nb) of electrons present in the bonding orbitals
♦ Write the number (Na) of electrons present in the anti-bonding orbitals
2. Find the difference Nb - Na
(Note that the ‘order of subtraction’ is important. Always subtract Na from Nb)
3. Then b.o is half of (Nb-Na)
• That is., $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}}}$
1. If we get a positive value for b.o, the molecule is stable
♦ A positive value indicates that Nb > Na
2. If we get a negative value for b.o, the molecule is unstable
♦ A negative value indicates that Na > Nb
3. If we get zero value for b.o, then also, the molecule is unstable
♦ Zero value indicates that Na = Nb
♦ The bonding contributions made by the Nb electrons will be nullified by the Na electrons
1. In H2, we have:
Nb = 2 and Na = 0
2. So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-0}{2}=1}}$
♦ This is a positive value
♦ So H2 is a stable molecule
• The b.o helps us to ascertain the nature of bond also. This can be explained in 3 steps:
1. If the b.o in a diatomic molecule is 1, the bond between those two atoms will be a single bond
2. If the b.o in a diatomic molecule is 2, the bond between those two atoms will be a double bond
3. If the b.o in a diatomic molecule is 3, the bond between those two atoms will be a triple bond
• We will see the mathematical proof for this in higher classes
• In our present case of H2 molecule, we obtained b.o as 1
♦ So there will be a single bond between the two H atoms
• This can be explained in 4 steps:
1. We know how to write the 'electronic configuration of atoms'
• The ‘electronic configuration of an atom’ depends on how the electrons in that atom are distributed in it’s atomic orbitals
2. In the same way, we can write:
• The ‘electronic configuration of a molecule’ depends on how the electrons in that molecule are distributed in it’s molecular orbitals
3. In our present case of H2 molecule, we have:
Both the electrons present in the σ1s orbital
4. So the electronic configuration is σ1s2.
This can be explained in steps:
1. Consider the square boxes in fig.4.190
♦ If a box contains two electrons, we say that: the electrons in that box are paired
✰ If two electrons are paired, their spins gets canceled
♦ If a box contains only one electron, we say that: The electron in that box is unpaired
✰ If an electron is unpaired, it’s spin will not be canceled
2. Consider a substance having unpaired electrons
♦ If that substance is kept in a magnetic field, the ‘spin of the unpaired electron’ gets affected
✰ The spin becomes aligned parallel to the applied magnetic field
✰ Due to this parallel alignment, the substance gets attracted towards the poles of the magnet
✰ So such substances having unpaired electrons are called paramagnetic substances
3. Consider a substance having all paired electrons
♦ All electron spins are canceled in such a substance. So the spins are not affected
♦ If this substance is kept in a magnetic field, it will be repelled away from the poles
✰ Such substances having all paired electrons are called diamagnetic substances
4. Both paramagnetism and diamagnetism are different from ferromagnetism
♦ In ferromagnetism:
✰ Substances like iron and nickel form permanent magnets
✰ Substances like iron and nickel get attracted to permanent magnets
♦ We see effects of ferromagnetism often in our day to day life
♦ But the effects of paramagnetism and diamagnetism are very small
✰ They can be detected only with the help of highly sensitive instruments in the laboratory
• Consider the hybridization concept that we saw in the previous sections
• We saw that:
♦ When two atoms combine to form molecules, new orbitals are formed in the central atom
✰ These new orbitals are called hybrid orbitals
♦ The orbitals of the 'outer atoms' overlap with the newly formed hybrid orbitals of the 'central atom'
♦ Thus new molecules are formed
• In our present case of molecular bond theory also, new orbitals are formed
✰ These new orbitals are called molecular orbitals
• There is a major difference between ‘hybrid orbitals’ and ‘molecular orbitals’. It can be explained in 3 steps:
1. The hybrid orbitals have a single center point
♦ The nucleus of the central atom is that center point
2. But the molecular orbitals have more than one center points
♦ The nuclei of the combining atoms are those center points
3. So we can write:
• A hybrid orbital has only one owner
♦ The owner is the central atom
• A molecular orbital has more than one owners
♦ The owners are the atoms which combine to form that molecule
• The above points will become more clear when we see ‘how molecular orbitals are formed’
1. Consider the 1s orbital of a H atom
♦ We will call this H atom as: HA
2. It is going to interact with the 1s orbital of another H atom
♦ We will call this H atom as: HB
3. So the two spheres comes closer and closer to each other
• What will happen when they interact?
• The following steps from (4) to () will give the answer:
4. To find the answer,
• We must first accept the ‘fundamental fact’: electrons behave as waves
• We must also accept the fact that, they are 3D waves
♦ That means the 'wave associated with an electron' occupies a three dimensional space
♦ The wave is not confined to a line (1D)
♦ The wave is not confined to a plane (2D)
5. But for simplicity, we will draw them as 2D waves in our present discussion
• Fig.4.184(a) below shows
♦ The wave associated with the electron in HA atom
♦ The wave associated with the electron in HB atom
 |
| Fig.4.184 |
• There are two types of addition
♦ When two waves are added, both 'types of addition' will take place
♦ We cannot choose one and stop the other from taking place
Type 1:
This can be explained in 4 steps:
(i) In fig.4.184(a), the crests of HA are in line with the crests of HB
♦ This is indicated by the red dotted lines
(ii) So naturally, the troughs will also be in line
(iii) When the two waves add, we get a single ‘new wave’
♦ This ‘new wave’ will be in favor of 'keeping the two H electrons together'
♦ So this ‘new wave’ will be in favor of ‘H2 bond formation’
(iv) We say that: this addition is constructive
Type 2:
This can be explained in 4 steps:
(i) In fig.4.184(b), the crests of HA are in line with the troughs of HB
♦ This is indicated by the green dotted lines
(ii) Here also, when the two waves add, we get a single ‘new wave’
♦ This ‘new wave’ will not be in favor of 'keeping the two H electrons together'
✰ This is because of the mismatch between crests and troughs
✰ They are ‘out of phase’
(iii) The two electrons will try to repel each other
♦ So this ‘new wave’ will not be in favor of ‘H2 bond formation’
(iv) We say that: this addition is destructive
7. When the two 1s spheres interact, they merge together.
• The 'results of the merger' can be written in 2 steps:
(i) Formation of new orbitals
• During merger, both constructive and destructive additions takes place
♦ The constructive addition gives rise to a new orbital called bonding orbital
♦ The destructive addition gives rise to a new orbital called anti-bonding orbital
■ The new orbitals thus formed are called molecular orbitals
(ii) Non-existence of old orbitals
• After the merger, the following two orbitals will no longer exist:
♦ The 1s orbital of HA
♦ The 1s orbital of HB
8. Let us see the actual shapes of the new molecular orbitals
It can be written in two steps (A) and (B):
A. Bonding orbital
(i) The constructive addition resulting in the formation of bonding orbital is shown in fig.4.185 below:
 |
| Fig.4.185 |
♦ The other 1s orbital belongs to the HB atom
♦ (Note that, the z-axis is taken as the inter-nuclear axis)
(ii) The resulting molecular orbital has an oval shape
♦ We have to give it a suitable name
♦ We see that, the two 1s spheres add 'in a end-to-end manner' along the inter-nuclear axis
♦ So the resulting molecular orbital is denoted by the symbol 'σ'
♦ Recall the ‘formation of σ bonds’ in the topic of hybridization (See fig.4.142 of section 4.25)
(iii) In or present case, the molecular orbital is formed by the merger of two 1s orbitals
♦ So we call the resulting molecular orbital as: σ1s
(iv) The above fig.4.185 is a 3D view. Such a view helps us to understand the actual shapes
• But in the present case, a 2D view will give us some extra details. It is shown in fig.4.186 below:
 |
| Fig.4.186 |
✰ So the nuclei are also visible. They are denoted by small red spheres
(v) In fig.4.186, consider the shape of σ1s
♦ Consider the region between the two nuclei
✰ This region is thicker
✰ This thicker region is at the exact middle portion between the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thicker portion is at the exact middle portion)
(vi) That means, the electrons will be spending more time in the middle portion between the two nuclei
♦ So both the nuclei has a strong influence on the two electrons
♦ This gives rise to a strong bond between the two nuclei
♦ Thus a strong H-H bond is formed, resulting in the H2 molecule
B. Anti-bonding orbital
(i) The destructive addition resulting in the formation of anti-bonding orbital is shown in fig.4.187 below:
 |
| Fig.4.187 |
♦ The other 1s orbital belongs to the HB atom
♦ (Note that, the z-axis is taken as the inter-nuclear axis)
(ii) The resulting molecular orbital has two separate lobes
♦ We have to give it a suitable name
♦ We see that, the two 1s spheres add 'in a end-to-end manner' along the inter-nuclear axis
♦ So the resulting molecular orbital is denoted by the 'σ' symbol
♦ Recall the ‘formation of σ bonds’ in the topic of hybridization (See fig.4.142 of section 4.25)
(iii) In our present case, the molecular orbital is formed by the merger of two 1s orbitals
♦ But the resulting molecular orbital is an anti-bonding orbital
♦ We have to distinguish it from the bonding orbital. For that, we give an extra '*' symbol
♦ So we call the resulting anti-bonding molecular orbital as: σ*1s
(iv) The above fig.4.186 is a 3D view. Such a view helps us to understand the actual shapes
• But in the present case, a 2D view will give us some extra details. It is shown in fig.4.188 below:
 |
| Fig.4.188 |
✰ So the nuclei are also visible. They are denoted by small red spheres
(v) In fig.4.188, consider the shape of σ*1s
♦ Consider the region between the two nuclei
✰ This region is thinner
✰ This thinner region is at the exact middle portion between the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thinner portion is at the exact middle portion)
(vi) In fig.4.188, consider the shape of σ*1s
♦ Consider the regions on the left and right sides of the two nuclei
✰ Those regions are thicker
✰ Those thicker regions are symmetrically distributed on either sides of the two nuclei
(In the 3D view, even if we show the nuclei, we will not recognize the fact that, the thicker portions are symmetrically distributed)
(vii) That means, the electrons will be spending more time away from the two nuclei
• It is clear that, in the σ*1s,
♦ The left side nucleus has no influence on the right side electron
♦ The right side nucleus has no effect on the left side electron
• The two 1s orbitals were independent before bond formation
• Now, even after the formation of the anti-bond, they are trying to separate away from each other
• This is because of the repulsion between the two nuclei
(viii) In fact, there is a definite plane between the two nuclei in the σ*1s
• This plane can be clearly marked in the 3D view. This is shown in the fig.4.189 below:
 |
| Fig.4.189 |
■ So it is clear that, anti-bonding will not help in the formation of H-H bond
(Note that in the 2D view, this plane will appear only as a very thin line. We will not be able to fully appreciate it's planar characteristics. So both 2D and 3D diagrams have advantages as well as disadvantages)
• The above eight steps help us to understand 'how simple molecular orbitals are formed'
• Right now, we have to learn some more details about the H2 molecule
• Initially we had
♦ 1s orbital of HA
♦ 1s orbital of HB
• After bond formation, in the H2 molecule, we do not have the 1s orbitals
• In the H2 molecule, we have
♦ The molecular orbital σ1s
✰ This is a bonding orbital
♦ The molecular orbital σ*1s
✰ This is a anti-bonding orbital
■ We want to know how the two electrons in the H2 molecule is distributed among the two molecular orbitals
• For that, we use a graphical method. It can be explained in 6 steps:
1. In this graphical method, the energy increases as we go upwards
[Recall that, this usually is the case. The orbitals (square boxes with two opposite arrows inside) with higher energies are shown towards the top. The orbitals with lower energies are shown towards the bottom]
• Such a graphical representation is shown in fig.4.190 below:
 |
| Fig.4.190 |
• Because, they have the same energy
3. The sloping green lines indicate that:
♦ The two 1s orbitals combine together to form σ1s
✰ This σ1s is shown at a lower level than that of the 1s orbitals
4. The sloping magenta lines indicate that:
♦ The two 1s orbitals combine together to form σ*1s
✰ This σ*1s is shown at a higher level than that of the 1s orbitals
5. Why is σ1s shown at a lower level than 1s?
• The answer can be written in 4 steps
(i) Consider the Earth-stone system
• The energy of the system is due to the attraction between the earth and the stone
♦ When the stone is high up above the ground, the energy will be high (less negative)
♦ When the stone is near the ground, the energy will be low (more negative)
• This type of 'increase or decrease in energy' depends on 'distance between Earth and the stone'
(ii) The 'energy can increase or decrease' depending on the masses also
♦ If the mass of the earth decrease, the energy will increase (become less negative)
♦ If the mass of the earth increases, the energy will decrease (become more negative)
(iii) Let us now consider a system of two charges
• It is similar to the Earth-stone system
• The ‘type of energy change’ described in (ii) can occur in the case of a two-charge system also. But instead of mass, we consider 'magnitude of the charge'
♦ If one of the charges is decreased in magnitude, the attraction will decrease
✰ Consequently, the energy of the system will increase (become less negative)
♦ If one of the charges is increased in magnitude, the attraction will increase
✰ Consequently, the energy of the system will decrease (become more negative)
(iv) Now we compare the charges in the two types of orbitals: 1s and σ1s
♦ In the 1s orbitals, the ‘attraction on electrons’ is exerted by a single nucleus
♦ In the σ1s orbital, the ‘attraction on electrons’ is exerted by two nuclei. This attraction is greater
• So the energy of the σ1s will be lower than that of 1s
• That is why σ1s is shown at a lower level than 1s
(We will see a more detailed explanation when we learn about 'interactions between charged particles' in physics classes)
6. Why is σ*1s shown at a higher level?
• The answer can be written in 6 steps:
(i) In (5), we saw that:
♦ There is greater attraction in σ1s than in 1s
(ii) We also saw that:
♦ Greater attraction leads to lesser energy
(iii) So the opposite must be true:
♦ Lesser attraction leads to greater energy
(iv) We can decrease the attraction further:
♦ Further decrease in attraction leads to still greater energy
(v) Lesser and lesser attraction will finally become repulsion
♦ So repulsion will lead to very high energy
(vi) Now we compare the two types of orbitals: 1s and σ*1s
♦ In 1s, there is attraction
♦ In σ*1s, there is actually repulsion between the two lobes
• So σ*1s will have a higher energy than 1s
• That is why σ*1s is shown at a higher level than 1s
Let us write a summary of the discussion so far in this section. It can be written in 3 steps
• Initially, the two hydrogen atoms HA and HB are independent
♦ The electron of HA resides in the 1s orbital of HA
♦ The electron of HB resides in the 1s orbital of HB
2. Bonded state
• The two atoms bond together to form one H2 molecule
♦ For the bond formation, the two 1s orbitals merge together to give two new orbitals
✰ The bonding orbital σ1s
✰ The anti-bonding orbital σ*1s
• After the bond formation, the initial 1s orbitals will no longer exist
3. Energy levels
♦ The σ1s has a lower energy than 1s
♦ The σ*1s has a higher energy than 1s
• So in the H2 molecule, there are no 1s orbitals
• The answer can be written in steps:
1. Obviously, they have no where else to go but the σ1s and σ*1s
♦ The two electrons will go to those new molecular orbitals
2. They will be looking for the orbital with the ‘least energy level’
♦ We have seen that, compared to the anti-bonding orbital , the bonding orbital has lesser energy
♦ So the two electrons will approach σ1s
3. First, one of the two electrons enter the σ1s
• We know that an atomic orbital can hold a maximum of two electrons
♦ This applies to molecular orbitals also
♦ So the second electron can also enter the σ1s
4. So the square denoting σ1s will contain two opposite arrows
♦ This is shown in fig.4.190(b) above
♦ The square denoting σ*1s will be left vacant
• The graphical representation in fig.4.190(b) helps us to calculate the ‘stability of the H2 molecule’
• This can be explained in 4 steps:
• This can be explained in 4 steps:
♦ Let Nb be the number of electrons occupying the bonding orbital σ1s
♦ Let Na be the number of electrons occupying the anti-bonding orbital σ*1s
2. If Nb > Na, we can write:
♦ The number of electrons trying to keep the two nuclei together is greater
♦ than
♦ The number of electrons trying to repel the two nuclei
■ This will result in a stable molecule
3. If Na > Nb, we can write:
♦ The number of electrons trying to repel the two nuclei is greater
♦ than
♦ The number of electrons trying to keep the two nuclei together
■ This will result in a unstable molecule
4. So in our present case of H2 molecule, we have:
♦ Nb = 2 and Na = 0
♦ So Nb > Na
■ Thus we can confirm that H2 is a stable molecule
• We can give a mathematical form for the above method
• Bond order (b.o) can be defined in 3 steps:
1. Number of electrons occupying each orbital:
♦ Write the number (Nb) of electrons present in the bonding orbitals
♦ Write the number (Na) of electrons present in the anti-bonding orbitals
2. Find the difference Nb - Na
(Note that the ‘order of subtraction’ is important. Always subtract Na from Nb)
3. Then b.o is half of (Nb-Na)
• That is., $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}}}$
• Let us see how b.o helps us to check whether a molecule is stable or not. It can be written in 3. steps
♦ A positive value indicates that Nb > Na
2. If we get a negative value for b.o, the molecule is unstable
♦ A negative value indicates that Na > Nb
3. If we get zero value for b.o, then also, the molecule is unstable
♦ Zero value indicates that Na = Nb
♦ The bonding contributions made by the Nb electrons will be nullified by the Na electrons
Let us calculate the b.o in our present case of H2 molecule. It can be written in 2 steps:
Nb = 2 and Na = 0
2. So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-0}{2}=1}}$
♦ This is a positive value
♦ So H2 is a stable molecule
Nature of the bond
1. If the b.o in a diatomic molecule is 1, the bond between those two atoms will be a single bond
2. If the b.o in a diatomic molecule is 2, the bond between those two atoms will be a double bond
3. If the b.o in a diatomic molecule is 3, the bond between those two atoms will be a triple bond
• We will see the mathematical proof for this in higher classes
• In our present case of H2 molecule, we obtained b.o as 1
♦ So there will be a single bond between the two H atoms
Electronic configuration of molecules
1. We know how to write the 'electronic configuration of atoms'
• The ‘electronic configuration of an atom’ depends on how the electrons in that atom are distributed in it’s atomic orbitals
2. In the same way, we can write:
• The ‘electronic configuration of a molecule’ depends on how the electrons in that molecule are distributed in it’s molecular orbitals
3. In our present case of H2 molecule, we have:
Both the electrons present in the σ1s orbital
4. So the electronic configuration is σ1s2.
Magnetic nature
1. Consider the square boxes in fig.4.190
♦ If a box contains two electrons, we say that: the electrons in that box are paired
✰ If two electrons are paired, their spins gets canceled
♦ If a box contains only one electron, we say that: The electron in that box is unpaired
✰ If an electron is unpaired, it’s spin will not be canceled
2. Consider a substance having unpaired electrons
♦ If that substance is kept in a magnetic field, the ‘spin of the unpaired electron’ gets affected
✰ The spin becomes aligned parallel to the applied magnetic field
✰ Due to this parallel alignment, the substance gets attracted towards the poles of the magnet
✰ So such substances having unpaired electrons are called paramagnetic substances
3. Consider a substance having all paired electrons
♦ All electron spins are canceled in such a substance. So the spins are not affected
♦ If this substance is kept in a magnetic field, it will be repelled away from the poles
✰ Such substances having all paired electrons are called diamagnetic substances
4. Both paramagnetism and diamagnetism are different from ferromagnetism
♦ In ferromagnetism:
✰ Substances like iron and nickel form permanent magnets
✰ Substances like iron and nickel get attracted to permanent magnets
♦ We see effects of ferromagnetism often in our day to day life
♦ But the effects of paramagnetism and diamagnetism are very small
✰ They can be detected only with the help of highly sensitive instruments in the laboratory
• We have seen how the 1s orbitals in two H atoms merge together to form σ1s and σ*1s
• He (helium) also possess 1s orbital
• What will happen when the 1s orbitals in two He atoms merge together?
• We will see it in the next section
• He (helium) also possess 1s orbital
• What will happen when the 1s orbitals in two He atoms merge together?
• We will see it in the next section
No comments:
Post a Comment