In the previous section 4.24, we saw the properties of hybrid orbitals. In this section, we will see how those orbitals can be used to make a satisfactory model of CH4. Later in this section, we will also see the basic details about sigma bonds
• Once we learn about hybrid orbitals, we can easily make the model. It can be written in 8 steps:
1. The C atom in CH4 is sp3 hybridized
2. We know that:
♦ In sp3 hybridization, there will be four hybrid orbitals
✰ Together, they form a tetrahedral shape
✰ The larger lobes will be directed towards the corners of a triangular pyramid
• This is shown in fig.4.136(a) below:
• In the fig.a, the smaller lobes are not shown
♦ This is to reduce congestion and thus obtain greater clarity
3. Distribution of electrons in the hybrid orbitals:
• This can be written in 3 steps:
(i) We know that, the sp3 hybrid orbitals are formed from 'one s orbital' and 'three p orbitals'
(ii) In the case of C atom, they are: 'one 2s orbital' and 'three 2p orbitals'
(iii) Before the hybridization, the orbitals mentioned in (ii) carry a total of four electrons
♦ After hybridization, the orbitals mentioned in (ii) will no longer exist
♦ Then what will happen to the four electrons?
Answer:
• The four electrons will be distributed among the four sp3 hybrid orbitals
♦ So each hybrid orbital will carry one electron
♦ This is indicated by the arrows in fig.4.136(a) above
4. Now, orbital overlapping can take place:
♦ the s orbital of the first H atom overlap onto the end of the first sp3 hybrid orbital of C
♦ the s orbital of the second H atom overlap onto the end of the second sp3 hybrid orbital of C
♦ the s orbital of the third H atom overlap onto the end of the third sp3 hybrid orbital of C
♦ the s orbital of the fourth H atom overlap onto the end of the fourth sp3 hybrid orbital of C
• This is shown in fig.4.136(b) above
5. In the fig.4.136(b), the H atoms are shown as orange spheres
• Then where is the C atom ?
• Answer can be written in 3 steps:
(i) The C atom is the central atom in CH4
♦ The central small red sphere is the nucleus of that C atom
(ii) The four hybrid orbitals also belong to the C atom
♦ Because, those hybrid orbitals are formed from the 2s and 2p orbitals of C
(iii) So we can write:
■ The small red sphere and the four hybrid orbitals together constitute the C atom
6. Since it is a tetrahedral shape, all the H-C-H bond angles will be 109.5o
• This is in agreement with the experimental results
• Thus we get a satisfactory model of the CH4 molecule
• All the four hybrid orbitals have the same energy
♦ So all the C-H bond energies in the CH4 will be equal
• All the four hybrid orbitals have the same length from the nucleus of C
♦ So all the four C-H bonds will be of the same length
7. The fig.4.136(b) is the final structure of CH4
• Let us compare this model with the model that we made in fig.4.131(c) in a previous section 4.23
♦ In fig.4.131(c), the lobes indicate the 2p orbitals
✰ In the above fig.4.136(b), the lobes indicate the sp3 hybrid orbitals
✰ After hybridization, the participating orbitals will no longer exist
✰ That is why we do not see the p orbitals in the above fig.4.136(b)
♦ In fig.4.131(c), there is a cyan sphere. It indicates the 2s orbital
✰ In the above fig.4.136(b), the cyan sphere is absent
✰ After hybridization, the participating orbitals will no longer exist
✰ That is why we do not see the cyan sphere in the above fig.4.136(b)
8. Fig.4.136(b) shows the Lewis dot structure of CH4
• Fig.4.136(c) shows the 2D representation of the 3d structure of CH4
• We have already seen how this 2D representation is obtained. See fig.4.86(a) in section 4.14.
1. The Lewis dot structure of C2H6 is shown in fig.4.137(a) below:
• We see that:
♦ There are two central atoms
♦ Both of them are C
♦ Three H atoms are attached to each of those C atoms
2. Both the C atoms in C2H6 are sp3 hybridized
♦ So each C will have four hybrid orbitals around it's nucleus
♦ Those orbitals will be arranged in a tetrahedral shape
3. We have seen that:
• The small red sphere and the four hybrid orbitals together constitute the C atom
• So one of the two C atoms is shown in fig.4.138(a) below:
• In the fig.a, the smaller lobes are not shown
♦ This is to reduce congestion and thus obtain greater clarity
• Two conditions must be satisfied:
♦ The small red sphere must lie exactly at the origin of the coordinate system
♦ The upward pointing orbital must lie exactly along the z-axis (blue axis)
(Orientations of the other three orbitals are not important as long as the four of them together form a tetrahedral shape)
4. Now rotate the tetrahedron. This can be explained in steps:
(i) The four orbitals together form a single rigid tetrahedral unit
(ii) The small red sphere is the pivot of rotation
(iii) The y-axis (green axis) is the axis of rotation
(iv) The curved yellow arrow shows the direction of rotation
(v) The angle of rotation should be exactly 90o
5. When the rotation is complete, the tetrahedron will attain a new position shown in fig.b
• In this final position:
♦ The orbital which initially pointed upwards has become horizontal
✰ It is now lying along the x-axis (red axis)
6. So we have a tetrahedron in fig.b
• We want a mirror image of that tetrahedron
• To obtain a 'required mirror image', we need to place the mirror in the 'correct position'
• In our present case, the 'correct position' can be specified using 2 steps:
(i) The x-axis should penetrate through the mirror
(ii) The the x-axis should be perpendicular to the 'plane of the mirror'
• Such a 'correct position' is shown in fig.4.138(c)
• The 'resulting mirror image' is also shown in the same fig.c
7. So now we have two tetrahedrons
• Remember that, each one of them is a C atom
• We want the two C atoms to bond together
• For that we use the following four steps:
(i) We have two orbitals lying along the x-axis
♦ One belongs to the 'original C atom'
♦ The other belongs to the 'mirror image C atom'
(ii) Move the mirror image towards the original
• The movement should be exactly along the x-axis
(iii) When an optimum distance is reached, overlapping takes place between the two orbitals mentioned in (i)
• 'overlapping' means that, there will be a particular region, which will belong to both the orbitals
• This region is called 'overlapping region'
(iv) The two electrons (one from each orbital) will then lie in that 'overlapping region'
• Thus the two electrons will belong to both the C atoms
• In this way, a bond is formed between those two C atoms
• This is shown in fig.4.139(a) below:
8. So in fig.4.139(a) above, we have two C atoms which are bonded together
Now bonding with H atoms can begin:
• Three H atoms will come and overlap with the free orbitals of the original C atom
• Another three H atoms will come and overlap with the free orbitals of the 'C atom which is the mirror image'
• Thus the molecule of C2H6 is formed
• This is shown in fig.4.139(b)
9. Consider the plane in fig.4.140 below
♦ The two C atoms lie on that plane
♦ Two H atoms also lie on that plane
♦ Two H atoms lie in front of the plane
♦ Two H atoms lie in the rear of the plane
(The plane is given a bit of transparency so that, the H atoms at the rear of the plane, also become visible)
• So the 2D representation of C2H6 will be as shown in the fig.4.137(b) which we saw earlier
10. Next we will see an interesting point. It can be written in 4 steps:
(i) Consider the final model in fig.4.139(b) above
• Let us consider it as two separate units
♦ The original C atom and it's three H atoms constitute the first unit
♦ The mirror image C atom and it's three H atoms constitute the second unit
(ii) Keep the first unit 'fixed'
♦ Rotate the second unit
♦ Nucleus of the second unit is the pivot of rotation
♦ x-axis is the axis of rotation
(iii) We can do this type of rotation with out causing any change to the structure
• This is shown in the animation in fig.4.141 below:
(iv) Consider the 'overlapping region' between the 'two hybrid orbitals lying along the x-axis'
• We can see that, all the while when rotation is taking place, there is no change in that 'over lapping region'
• That is why, such a rotation is possible
• It can be explained in 9 steps:
1. The fig.4.142(a) below shows the final structure of C2H6
2. Consider the hydrogen atom marked as 'H'
• The yellow line passes through two important points:
♦ The nucleus of H
♦ The nucleus of C (the small red sphere)
■ So the yellow line is the internuclear axis
• We can see that, the two orbitals (s orbital of H and sp3 hybrid orbital of C) overlap in a end-to-end manner along the internuclear axis
♦ We call it: a sigma bond
3. Consider the hydrogen atom marked as H in fig.b
• The yellow line passes through two important points:
♦ The nucleus of H
♦ The nucleus of C (the small red sphere)
■ So the yellow line is the internuclear axis
• We can see that, the two orbitals (s orbital of H and sp3 hybrid orbital of C) do not overlap in a end-to-end manner
♦ The overlap is not along the internuclear axis
♦ We can not call it: a sigma bond
4. So we can write the definition:
■ The bond in which the orbitals overlap in a end-to-end manner along the internuclear axis is called sigma bond
♦ In symbolic form, it is written as: 𝛔 bond
5. It is clear that:
♦ All the C-H bonds in C2H6 are 𝛔 bonds
✰ Each of those bonds is between a 'sp3 hybrid orbital of C' and a 's orbital of H'
✰ So each is called: sp3-s 𝛔 bond
♦ All the C-H bonds in CH4 are also 𝛔 bonds
✰ Each of those bonds is between a 'sp3 hybrid orbital of C' and a 's orbital of H'
✰ So each is called: sp3-s 𝛔 bond
6. Another 𝛔 bond in the C2H6 molecule:
• This can be explained in 6 steps
(i) We have two orbitals which lie along the x-axis
♦ One belongs to the original C atom
♦ The other belongs to the mirror image C atom
(ii) The x-axis passes through both the carbon nuclei
♦ So x-axis is the internuclear axis here
(iii) The bond between the two orbitals is in a end-to-end manner
(iv) The bond is along the x-axis (internuclear axis)
(v) So this bond is a 𝛔 bond
(vi) This bond is between two sp3 hybrid orbitals
• So it is called: sp3-sp3 𝛔 bond
7. So we have seen that:
• A 𝛔 bond can take place between:
♦ a hybrid orbital and a s orbital
✰ The C-H bonds in CH4 and C2H6 are examples
♦ two hybrid orbitals
✰ The C-C bond in C2H6 is an example
8. In addition to the above two, there is one more possibility. It can be explained in 5 steps:
(i) Consider two s orbitals
All s orbitals are spherical in shape
(ii) So two s orbitals can overlap in any direction
(iii) Whatever be the direction, we can always draw a line connecting the two nuclei
• This line is the internuclear axis
(iv) Whatever be the direction, the overlapping region will lie along the internuclear axis
This is shown in fig.4.143 below. It shows three possibilities
(v) So whatever be the direction, it will be a 𝛔 bond
9. So we can add this information to what we wrote in (7). The modified form of (7) is:
• A 𝛔 bond can take place between:
♦ a hybrid orbital and a s orbital
✰ The C-H bonds in CH4 and C2H6 are examples
✰ All those C-H bonds are sp3-s 𝛔 bonds
♦ two hybrid orbitals
✰ The C-C bond in C2H6 is an example
✰ That C-C bond is a sp3-sp3 𝛔 bond
♦ two s orbitals
✰ The H-H bond in H2 is an example
✰ That H-H bond is a s-s 𝛔 bond
• Once we learn about hybrid orbitals, we can easily make the model. It can be written in 8 steps:
1. The C atom in CH4 is sp3 hybridized
2. We know that:
♦ In sp3 hybridization, there will be four hybrid orbitals
✰ Together, they form a tetrahedral shape
✰ The larger lobes will be directed towards the corners of a triangular pyramid
• This is shown in fig.4.136(a) below:
 |
| Fig.4.136 |
♦ This is to reduce congestion and thus obtain greater clarity
3. Distribution of electrons in the hybrid orbitals:
• This can be written in 3 steps:
(i) We know that, the sp3 hybrid orbitals are formed from 'one s orbital' and 'three p orbitals'
(ii) In the case of C atom, they are: 'one 2s orbital' and 'three 2p orbitals'
(iii) Before the hybridization, the orbitals mentioned in (ii) carry a total of four electrons
♦ After hybridization, the orbitals mentioned in (ii) will no longer exist
♦ Then what will happen to the four electrons?
Answer:
• The four electrons will be distributed among the four sp3 hybrid orbitals
♦ So each hybrid orbital will carry one electron
♦ This is indicated by the arrows in fig.4.136(a) above
4. Now, orbital overlapping can take place:
♦ the s orbital of the first H atom overlap onto the end of the first sp3 hybrid orbital of C
♦ the s orbital of the second H atom overlap onto the end of the second sp3 hybrid orbital of C
♦ the s orbital of the third H atom overlap onto the end of the third sp3 hybrid orbital of C
♦ the s orbital of the fourth H atom overlap onto the end of the fourth sp3 hybrid orbital of C
• This is shown in fig.4.136(b) above
5. In the fig.4.136(b), the H atoms are shown as orange spheres
• Then where is the C atom ?
• Answer can be written in 3 steps:
(i) The C atom is the central atom in CH4
♦ The central small red sphere is the nucleus of that C atom
(ii) The four hybrid orbitals also belong to the C atom
♦ Because, those hybrid orbitals are formed from the 2s and 2p orbitals of C
(iii) So we can write:
■ The small red sphere and the four hybrid orbitals together constitute the C atom
6. Since it is a tetrahedral shape, all the H-C-H bond angles will be 109.5o
• This is in agreement with the experimental results
• Thus we get a satisfactory model of the CH4 molecule
• All the four hybrid orbitals have the same energy
♦ So all the C-H bond energies in the CH4 will be equal
• All the four hybrid orbitals have the same length from the nucleus of C
♦ So all the four C-H bonds will be of the same length
7. The fig.4.136(b) is the final structure of CH4
• Let us compare this model with the model that we made in fig.4.131(c) in a previous section 4.23
♦ In fig.4.131(c), the lobes indicate the 2p orbitals
✰ In the above fig.4.136(b), the lobes indicate the sp3 hybrid orbitals
✰ After hybridization, the participating orbitals will no longer exist
✰ That is why we do not see the p orbitals in the above fig.4.136(b)
♦ In fig.4.131(c), there is a cyan sphere. It indicates the 2s orbital
✰ In the above fig.4.136(b), the cyan sphere is absent
✰ After hybridization, the participating orbitals will no longer exist
✰ That is why we do not see the cyan sphere in the above fig.4.136(b)
8. Fig.4.136(b) shows the Lewis dot structure of CH4
• Fig.4.136(c) shows the 2D representation of the 3d structure of CH4
• We have already seen how this 2D representation is obtained. See fig.4.86(a) in section 4.14.
Next we will see the molecule of C2H6 (ethane). It can be written in 10 steps:
 |
| Fig.4.137 |
♦ There are two central atoms
♦ Both of them are C
♦ Three H atoms are attached to each of those C atoms
2. Both the C atoms in C2H6 are sp3 hybridized
♦ So each C will have four hybrid orbitals around it's nucleus
♦ Those orbitals will be arranged in a tetrahedral shape
3. We have seen that:
• The small red sphere and the four hybrid orbitals together constitute the C atom
• So one of the two C atoms is shown in fig.4.138(a) below:
 |
| Fig.4.138 |
♦ This is to reduce congestion and thus obtain greater clarity
• Two conditions must be satisfied:
♦ The small red sphere must lie exactly at the origin of the coordinate system
♦ The upward pointing orbital must lie exactly along the z-axis (blue axis)
(Orientations of the other three orbitals are not important as long as the four of them together form a tetrahedral shape)
4. Now rotate the tetrahedron. This can be explained in steps:
(i) The four orbitals together form a single rigid tetrahedral unit
(ii) The small red sphere is the pivot of rotation
(iii) The y-axis (green axis) is the axis of rotation
(iv) The curved yellow arrow shows the direction of rotation
(v) The angle of rotation should be exactly 90o
5. When the rotation is complete, the tetrahedron will attain a new position shown in fig.b
• In this final position:
♦ The orbital which initially pointed upwards has become horizontal
✰ It is now lying along the x-axis (red axis)
6. So we have a tetrahedron in fig.b
• We want a mirror image of that tetrahedron
• To obtain a 'required mirror image', we need to place the mirror in the 'correct position'
• In our present case, the 'correct position' can be specified using 2 steps:
(i) The x-axis should penetrate through the mirror
(ii) The the x-axis should be perpendicular to the 'plane of the mirror'
• Such a 'correct position' is shown in fig.4.138(c)
• The 'resulting mirror image' is also shown in the same fig.c
7. So now we have two tetrahedrons
• Remember that, each one of them is a C atom
• We want the two C atoms to bond together
• For that we use the following four steps:
(i) We have two orbitals lying along the x-axis
♦ One belongs to the 'original C atom'
♦ The other belongs to the 'mirror image C atom'
(ii) Move the mirror image towards the original
• The movement should be exactly along the x-axis
(iii) When an optimum distance is reached, overlapping takes place between the two orbitals mentioned in (i)
• 'overlapping' means that, there will be a particular region, which will belong to both the orbitals
• This region is called 'overlapping region'
(iv) The two electrons (one from each orbital) will then lie in that 'overlapping region'
• Thus the two electrons will belong to both the C atoms
• In this way, a bond is formed between those two C atoms
• This is shown in fig.4.139(a) below:
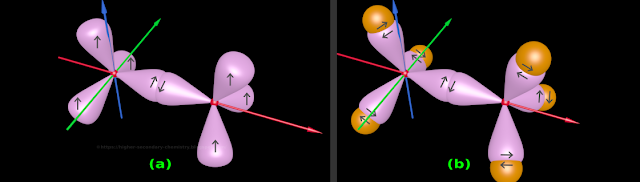 |
| Fig.4.139 |
Now bonding with H atoms can begin:
• Three H atoms will come and overlap with the free orbitals of the original C atom
• Another three H atoms will come and overlap with the free orbitals of the 'C atom which is the mirror image'
• Thus the molecule of C2H6 is formed
• This is shown in fig.4.139(b)
9. Consider the plane in fig.4.140 below
♦ The two C atoms lie on that plane
♦ Two H atoms also lie on that plane
♦ Two H atoms lie in front of the plane
♦ Two H atoms lie in the rear of the plane
(The plane is given a bit of transparency so that, the H atoms at the rear of the plane, also become visible)
 |
| Fig.4.140 |
10. Next we will see an interesting point. It can be written in 4 steps:
(i) Consider the final model in fig.4.139(b) above
• Let us consider it as two separate units
♦ The original C atom and it's three H atoms constitute the first unit
♦ The mirror image C atom and it's three H atoms constitute the second unit
(ii) Keep the first unit 'fixed'
♦ Rotate the second unit
♦ Nucleus of the second unit is the pivot of rotation
♦ x-axis is the axis of rotation
(iii) We can do this type of rotation with out causing any change to the structure
• This is shown in the animation in fig.4.141 below:
 |
| Fig.4.141 |
• We can see that, all the while when rotation is taking place, there is no change in that 'over lapping region'
• That is why, such a rotation is possible
• The structure of C2H6 gives us an opportunity to learn about sigma bond
1. The fig.4.142(a) below shows the final structure of C2H6
 |
| Fig.4.142 |
• The yellow line passes through two important points:
♦ The nucleus of H
♦ The nucleus of C (the small red sphere)
■ So the yellow line is the internuclear axis
• We can see that, the two orbitals (s orbital of H and sp3 hybrid orbital of C) overlap in a end-to-end manner along the internuclear axis
♦ We call it: a sigma bond
3. Consider the hydrogen atom marked as H in fig.b
• The yellow line passes through two important points:
♦ The nucleus of H
♦ The nucleus of C (the small red sphere)
■ So the yellow line is the internuclear axis
• We can see that, the two orbitals (s orbital of H and sp3 hybrid orbital of C) do not overlap in a end-to-end manner
♦ The overlap is not along the internuclear axis
♦ We can not call it: a sigma bond
4. So we can write the definition:
■ The bond in which the orbitals overlap in a end-to-end manner along the internuclear axis is called sigma bond
♦ In symbolic form, it is written as: 𝛔 bond
5. It is clear that:
♦ All the C-H bonds in C2H6 are 𝛔 bonds
✰ Each of those bonds is between a 'sp3 hybrid orbital of C' and a 's orbital of H'
✰ So each is called: sp3-s 𝛔 bond
♦ All the C-H bonds in CH4 are also 𝛔 bonds
✰ Each of those bonds is between a 'sp3 hybrid orbital of C' and a 's orbital of H'
✰ So each is called: sp3-s 𝛔 bond
6. Another 𝛔 bond in the C2H6 molecule:
• This can be explained in 6 steps
(i) We have two orbitals which lie along the x-axis
♦ One belongs to the original C atom
♦ The other belongs to the mirror image C atom
(ii) The x-axis passes through both the carbon nuclei
♦ So x-axis is the internuclear axis here
(iii) The bond between the two orbitals is in a end-to-end manner
(iv) The bond is along the x-axis (internuclear axis)
(v) So this bond is a 𝛔 bond
(vi) This bond is between two sp3 hybrid orbitals
• So it is called: sp3-sp3 𝛔 bond
7. So we have seen that:
• A 𝛔 bond can take place between:
♦ a hybrid orbital and a s orbital
✰ The C-H bonds in CH4 and C2H6 are examples
♦ two hybrid orbitals
✰ The C-C bond in C2H6 is an example
8. In addition to the above two, there is one more possibility. It can be explained in 5 steps:
(i) Consider two s orbitals
All s orbitals are spherical in shape
(ii) So two s orbitals can overlap in any direction
(iii) Whatever be the direction, we can always draw a line connecting the two nuclei
• This line is the internuclear axis
(iv) Whatever be the direction, the overlapping region will lie along the internuclear axis
This is shown in fig.4.143 below. It shows three possibilities
 |
| Fig.4.143 |
9. So we can add this information to what we wrote in (7). The modified form of (7) is:
• A 𝛔 bond can take place between:
♦ a hybrid orbital and a s orbital
✰ The C-H bonds in CH4 and C2H6 are examples
✰ All those C-H bonds are sp3-s 𝛔 bonds
♦ two hybrid orbitals
✰ The C-C bond in C2H6 is an example
✰ That C-C bond is a sp3-sp3 𝛔 bond
♦ two s orbitals
✰ The H-H bond in H2 is an example
✰ That H-H bond is a s-s 𝛔 bond
• In the next section, we will see the structure of C2H4 (ethene)
No comments:
Post a Comment