• In the previous section 4.32, we saw how the 1s orbitals in two H atoms merge together to form σ1s and σ*1s
• He (helium) also possess 1s orbital
• What will happen when the 1s orbitals in two He atoms merge together?
• We will see it in the present section
The case of He can be written in 9 steps:
1. Like H, the He also has only one orbital: The 1s
• So when two He atoms combine to form a He2 molecule, the two 1s orbitals will merge
2. The 1s of the first He atom merge with the 1s of the second He atom
• This merger is same as what we saw in the previous section
♦ The constructive addition results in the bonding orbital σ1s (Figs.4.185 and 186 of the previous section)
♦ The destructive addition results in the anti-bonding orbital σ*1s (Figs.4.187, 188 and 189 of the previous section)
3. So we can write:
♦ In He2 molecule, there will be
✰ A bonding orbital σ1s
✰ A anti-bonding orbital σ*1s
4. Thus we know the orbitals present in the He2 molecule
• So now we can distribute the electrons into those orbitals
• In a single He atom, there are two electrons
• So in a He2 molecule, there will be four electrons
♦ Two of those electrons will go to the orbital of lowest energy: The σ1s
♦ The remaining two has no where else to go but the σ*1s
♦ Thus we get the arrangement shown in fig.4.191(a) below:
• Based on fig.4.191 above, we can determine five items:
(i) Bond order in He2 molecule
(ii) Stability of He2 molecule
(iii) Nature of bond in He2 molecule
(iv) Electronic configuration of He2 molecule
(v) Magnetic nature of He2 molecule
The following steps from (5) to (9) shows the calculations related to the five items:
5. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In He2, we have:
Nb = 2 and Na = 2
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-2}{2}=0}}$
6. Next we determine the stability. This can be written in 3 steps:
(i) In the previous section, we saw that:
♦ If we get a positive value for b.o, the molecule is stable
♦ If we get a negative value for b.o, the molecule is unstable
♦ If we get zero value for b.o, then also, the molecule is unstable
(ii) From (5) above, we have:
b.o of He2 = 0
(iii) So we can write: He2 is a unstable molecule
• That means:
♦ Even if we combine two He atoms forcefully, the resulting He2 will not be stable
♦ The electrons in the σ1s will try to keep the two atoms together
✰ They do this by exerting an attractive force
♦ The electrons in the σ*1s will try to push away the two atoms
✰ They do this by exerting a repulsive force
♦ In He2, the two forces are equal and opposite
♦ So He2 will not exist
7. Next we determine the nature of bond in He2 molecule. This can be written in 3 steps:
(i) In the previous section, we saw that:
♦ The bond between two atoms in a diatomic molecule will be:
✰ Single bond if the b.o in that molecule is 1
✰ Double bond if the b.o in that molecule is 2
✰ Triple bond if the b.o in that molecule is 3
(ii) From (5) above, we have:
b.o of He2 = 0
(iii) So there is no bond between the two He atoms
• In fact, since we determined in (6) that He2 is unstable, there is no point in investigating the nature of bond
8. Next we determine the Electronic configuration of He2 molecule. This can be written in 3 steps:
(i) In the previous section we saw that:
• The ‘electronic configuration of a molecule’ depends on how the electrons in that molecule are distributed in it’s molecular orbitals
(ii) In our present case of He2 molecule, we have:
♦ Two electrons present in the σ1s orbital
♦ Two electrons present in the σ*1s orbital
(iii) So the electronic configuration is (σ1s)2 (σ*1s)2.
9. Next we determine the Magnetic nature of He2 molecule. This can be written in 2 steps:
♦ Even if one square box contain unpaired electron, that substance will be paramagnetic
(ii) In our present case, in fig.4.191(a), we see that all boxes contain paired electrons
♦ So He2 is diamagnetic
• Note that the elements H and He are the first two elements of the periodic table
• So next, we must be considering the third element Li (Lithium)
• We must be considering the Li2 molecule
• But before that, we have to consider another two items. It can be explained in 5 steps:
1. In H there is only one atomic orbital: the 1s
♦ So in H2 there are only two molecular orbitals: σ1s and σ*1s
2. In He also, there is only one atomic orbital: the 1s
♦ So in He2 also, there are only two molecular orbitals: σ1s and σ*1s
3. In Li, there is one more orbital in addition to 1s. It is the 2s
♦ So in Li2, there will be more molecular orbitals in addition to σ1s and σ*1s
4. In both H2 and He2, there are only σ1s and σ*1s
■ Are there any other substances 'which have only σ1s and σ*1s ?
Answer: There indeed exists such substances
5. So it is better to discuss about them first before taking up Li2
• The substances that we are going to discuss are: H2+ (hydrogen ion) and He2+ (helium ion)
1. We know that H2+ is formed when one electron is knocked off from H2
• So to obtain the electronic configuration of H2+, we simply do this:
♦ From the electronic configuration of H2, remove one electron
♦ We saw the electronic configuration of H2 in fig.4.190(b) of the previous section
2. So there will be only one arrow in the σ1s square
• This is shown in fig.4.192(a) below:
• Now we can determine the five items:
(i) Bond order in H2+ ion
(ii) Stability of H2+ ion
(iii) Nature of bond in H2+ ion
(iv) Electronic configuration of H2+ ion
(v) Magnetic nature of H2+ ion
The following steps from (3) to (7) shows the calculations related to the five items:
3. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In H2+, we have:
Nb = 1 and Na = 0
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{1-0}{2}=0.5}}$
4. Next we determine the stability. This can be written in 3 steps:
(i) From (3) above, we have:
b.o of H2+ = 0.5
• This is greater than zero. So the ion does exist
(ii) We can write:
♦ H2 has a b.o of 1
♦ H2+ has a b.o of 0.5
♦ That means H2+ ion is less stable than H2 molecule
(iii) H2+ can be 'kept with out decomposing' only if we place it inside a special container so that, there is no contact with oxygen, moisture etc.,
5. Next we determine the nature of bond in H2+ ion. This can be written in 2 steps:
(i) From (3) above, we have:
b.o of H2+ = 0.5
(ii) This b.o is not a whole number
♦ So in this case, we cannot use b.o to write whether it has a single, double or triple bond
6. Next we determine the electronic configuration of H2+ ion. This can be written in 2 steps:
(i) In H2+ ion, we have:
♦ One electron present in the σ1s orbital
(ii) So the electronic configuration is (σ*1s)1
7. Next we determine the magnetic nature of H2+ ion
• In fig.4.192(a), we see that the box corresponding to σ1s contain an unpaired electron
♦ So H2+ ion is paramagnetic
1. We know that He2+ is formed when one electron is knocked off from He2
• So to obtain the electronic configuration of He2+, we simply do this:
♦ From the electronic configuration of He2, remove one electron
♦ We saw the electronic configuration of He2 in fig.4.191 at the beginning of this section
2. So there will be only one arrow in the upper square
This is shown in fig.4.192(b) above
■ Why do we remove electron from σ*1s ? Why not from σ1s ?
• The answer can be written in 2 steps:
(i) While adding electrons into the orbitals, we follow a definite order:
♦ Orbitals of lower energies first
(ii) So while removing electrons from the orbitals, we follow the reverse order
♦ Orbitals with higher energies first
• Now we can determine the five items:
(i) Bond order in He2+ ion
(ii) Stability of He2+ ion
(iii) Nature of bond in He2+ ion
(iv) Electronic configuration of He2+ ion
(v) Magnetic nature of He2+ ion
The following steps from (3) to (7) shows the calculations related to the five items:
3. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In He2+, we have:
Nb = 2 and Na = 1
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-1}{2}=0.5}}$
4. Next we determine the stability. This can be written in 3 steps:
(i) From (3) above, we have:
b.o of He2+ = 0.5
• This is greater than zero. So the ion does exist
(ii) We can write:
♦He2 has a b.o of 0
♦ He2+ has a b.o of 0.5
♦ That means He2+ ion is more stable than He2 molecule
• But note that, He2+ is less stable than H2
(iii) He2+ can be 'kept with out decomposing' only if we place it inside a special container so that, there is no contact with oxygen, moisture etc.,
5. Next we determine the nature of bond in He2+ ion. This can be written in 2 steps:
(i) From (3) above, we have:
b.o of He2+ = 0.5
(ii) This b.o is not a whole number
♦ So in this case, we cannot use b.o to write whether it has a single, double or triple bond
6. Next we determine the electronic configuration of He2+ ion. This can be written in 2 steps:
(i) In He2+ ion, we have:
♦ Two electrons present in the σ1s orbital
♦ One electron present in the σ*1s orbital
(ii) So the electronic configuration is (σ1s)2 (σ*1s)1
7. Next we determine the magnetic nature of He2+ ion
• In fig.4.192(b), we see that the box corresponding to σ*1s contain an unpaired electron
♦ So He2+ ion is paramagnetic
• He (helium) also possess 1s orbital
• What will happen when the 1s orbitals in two He atoms merge together?
• We will see it in the present section
The case of He can be written in 9 steps:
1. Like H, the He also has only one orbital: The 1s
• So when two He atoms combine to form a He2 molecule, the two 1s orbitals will merge
2. The 1s of the first He atom merge with the 1s of the second He atom
• This merger is same as what we saw in the previous section
♦ The constructive addition results in the bonding orbital σ1s (Figs.4.185 and 186 of the previous section)
♦ The destructive addition results in the anti-bonding orbital σ*1s (Figs.4.187, 188 and 189 of the previous section)
3. So we can write:
♦ In He2 molecule, there will be
✰ A bonding orbital σ1s
✰ A anti-bonding orbital σ*1s
4. Thus we know the orbitals present in the He2 molecule
• So now we can distribute the electrons into those orbitals
• In a single He atom, there are two electrons
• So in a He2 molecule, there will be four electrons
♦ Two of those electrons will go to the orbital of lowest energy: The σ1s
♦ The remaining two has no where else to go but the σ*1s
♦ Thus we get the arrangement shown in fig.4.191(a) below:
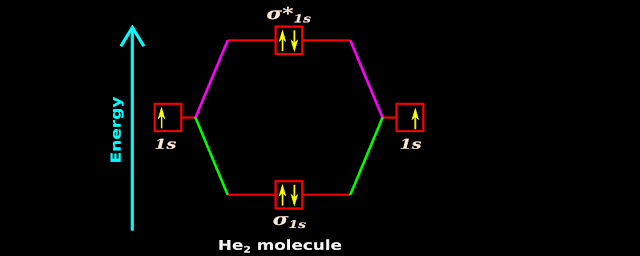 |
| Fig.4.191 |
(i) Bond order in He2 molecule
(ii) Stability of He2 molecule
(iii) Nature of bond in He2 molecule
(iv) Electronic configuration of He2 molecule
(v) Magnetic nature of He2 molecule
The following steps from (5) to (9) shows the calculations related to the five items:
5. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In He2, we have:
Nb = 2 and Na = 2
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-2}{2}=0}}$
6. Next we determine the stability. This can be written in 3 steps:
(i) In the previous section, we saw that:
♦ If we get a positive value for b.o, the molecule is stable
♦ If we get a negative value for b.o, the molecule is unstable
♦ If we get zero value for b.o, then also, the molecule is unstable
(ii) From (5) above, we have:
b.o of He2 = 0
(iii) So we can write: He2 is a unstable molecule
• That means:
♦ Even if we combine two He atoms forcefully, the resulting He2 will not be stable
♦ The electrons in the σ1s will try to keep the two atoms together
✰ They do this by exerting an attractive force
♦ The electrons in the σ*1s will try to push away the two atoms
✰ They do this by exerting a repulsive force
♦ In He2, the two forces are equal and opposite
♦ So He2 will not exist
7. Next we determine the nature of bond in He2 molecule. This can be written in 3 steps:
(i) In the previous section, we saw that:
♦ The bond between two atoms in a diatomic molecule will be:
✰ Single bond if the b.o in that molecule is 1
✰ Double bond if the b.o in that molecule is 2
✰ Triple bond if the b.o in that molecule is 3
(ii) From (5) above, we have:
b.o of He2 = 0
(iii) So there is no bond between the two He atoms
• In fact, since we determined in (6) that He2 is unstable, there is no point in investigating the nature of bond
8. Next we determine the Electronic configuration of He2 molecule. This can be written in 3 steps:
(i) In the previous section we saw that:
• The ‘electronic configuration of a molecule’ depends on how the electrons in that molecule are distributed in it’s molecular orbitals
(ii) In our present case of He2 molecule, we have:
♦ Two electrons present in the σ1s orbital
♦ Two electrons present in the σ*1s orbital
(iii) So the electronic configuration is (σ1s)2 (σ*1s)2.
9. Next we determine the Magnetic nature of He2 molecule. This can be written in 2 steps:
(i) In the previous section we saw that:
♦ If all the square boxes have paired electrons, that substance will be diamagnetic♦ Even if one square box contain unpaired electron, that substance will be paramagnetic
(ii) In our present case, in fig.4.191(a), we see that all boxes contain paired electrons
♦ So He2 is diamagnetic
• We have completed the discussion on two molecules H2 and He2
• So next, we must be considering the third element Li (Lithium)
• We must be considering the Li2 molecule
• But before that, we have to consider another two items. It can be explained in 5 steps:
1. In H there is only one atomic orbital: the 1s
♦ So in H2 there are only two molecular orbitals: σ1s and σ*1s
2. In He also, there is only one atomic orbital: the 1s
♦ So in He2 also, there are only two molecular orbitals: σ1s and σ*1s
3. In Li, there is one more orbital in addition to 1s. It is the 2s
♦ So in Li2, there will be more molecular orbitals in addition to σ1s and σ*1s
4. In both H2 and He2, there are only σ1s and σ*1s
■ Are there any other substances 'which have only σ1s and σ*1s ?
Answer: There indeed exists such substances
5. So it is better to discuss about them first before taking up Li2
• The substances that we are going to discuss are: H2+ (hydrogen ion) and He2+ (helium ion)
First we will take up H2+. It can be written in 7 steps:
• So to obtain the electronic configuration of H2+, we simply do this:
♦ From the electronic configuration of H2, remove one electron
♦ We saw the electronic configuration of H2 in fig.4.190(b) of the previous section
2. So there will be only one arrow in the σ1s square
• This is shown in fig.4.192(a) below:
 |
| Fig.4.192 |
(i) Bond order in H2+ ion
(ii) Stability of H2+ ion
(iii) Nature of bond in H2+ ion
(iv) Electronic configuration of H2+ ion
(v) Magnetic nature of H2+ ion
The following steps from (3) to (7) shows the calculations related to the five items:
3. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In H2+, we have:
Nb = 1 and Na = 0
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{1-0}{2}=0.5}}$
4. Next we determine the stability. This can be written in 3 steps:
(i) From (3) above, we have:
b.o of H2+ = 0.5
• This is greater than zero. So the ion does exist
(ii) We can write:
♦ H2 has a b.o of 1
♦ H2+ has a b.o of 0.5
♦ That means H2+ ion is less stable than H2 molecule
(iii) H2+ can be 'kept with out decomposing' only if we place it inside a special container so that, there is no contact with oxygen, moisture etc.,
5. Next we determine the nature of bond in H2+ ion. This can be written in 2 steps:
(i) From (3) above, we have:
b.o of H2+ = 0.5
(ii) This b.o is not a whole number
♦ So in this case, we cannot use b.o to write whether it has a single, double or triple bond
6. Next we determine the electronic configuration of H2+ ion. This can be written in 2 steps:
(i) In H2+ ion, we have:
♦ One electron present in the σ1s orbital
(ii) So the electronic configuration is (σ*1s)1
7. Next we determine the magnetic nature of H2+ ion
• In fig.4.192(a), we see that the box corresponding to σ1s contain an unpaired electron
♦ So H2+ ion is paramagnetic
Next we will take up He2+ it can be written in 7 steps:
• So to obtain the electronic configuration of He2+, we simply do this:
♦ From the electronic configuration of He2, remove one electron
♦ We saw the electronic configuration of He2 in fig.4.191 at the beginning of this section
2. So there will be only one arrow in the upper square
This is shown in fig.4.192(b) above
■ Why do we remove electron from σ*1s ? Why not from σ1s ?
• The answer can be written in 2 steps:
(i) While adding electrons into the orbitals, we follow a definite order:
♦ Orbitals of lower energies first
(ii) So while removing electrons from the orbitals, we follow the reverse order
♦ Orbitals with higher energies first
• Now we can determine the five items:
(i) Bond order in He2+ ion
(ii) Stability of He2+ ion
(iii) Nature of bond in He2+ ion
(iv) Electronic configuration of He2+ ion
(v) Magnetic nature of He2+ ion
The following steps from (3) to (7) shows the calculations related to the five items:
3. First we determine the bond order (b.o). It can be written in 2 steps:
(i) In He2+, we have:
Nb = 2 and Na = 1
(ii) So $\mathbf\small{\rm{b.o=\frac{N_b-Na}{2}=\frac{2-1}{2}=0.5}}$
4. Next we determine the stability. This can be written in 3 steps:
(i) From (3) above, we have:
b.o of He2+ = 0.5
• This is greater than zero. So the ion does exist
(ii) We can write:
♦He2 has a b.o of 0
♦ He2+ has a b.o of 0.5
♦ That means He2+ ion is more stable than He2 molecule
• But note that, He2+ is less stable than H2
(iii) He2+ can be 'kept with out decomposing' only if we place it inside a special container so that, there is no contact with oxygen, moisture etc.,
5. Next we determine the nature of bond in He2+ ion. This can be written in 2 steps:
(i) From (3) above, we have:
b.o of He2+ = 0.5
(ii) This b.o is not a whole number
♦ So in this case, we cannot use b.o to write whether it has a single, double or triple bond
6. Next we determine the electronic configuration of He2+ ion. This can be written in 2 steps:
(i) In He2+ ion, we have:
♦ Two electrons present in the σ1s orbital
♦ One electron present in the σ*1s orbital
(ii) So the electronic configuration is (σ1s)2 (σ*1s)1
7. Next we determine the magnetic nature of He2+ ion
• In fig.4.192(b), we see that the box corresponding to σ*1s contain an unpaired electron
♦ So He2+ ion is paramagnetic
• In the next section, we will see the details related to Li2 molecule
No comments:
Post a Comment