In the previous section 4.23, we saw a possible model of the CH4 molecule. We also saw the drawbacks of that model. In this section, we will see how scientists were able to overcome those drawbacks
• Linus Pauling put forward the concept of hybridization. The basics of this concept can be explained in steps:
1. In the valence shell of the C atom, we have:
♦ One 2s orbital
✰ This is completely filled
♦ One 2px orbital
✰ This is half filled
♦ One 2py orbital
✰ This is half filled
♦ One 2pz orbital
✰ This is empty
2. So there are a total of four orbitals
• These four orbitals mix together
• The result is the formation of some new orbitals
• These new orbitals are called hybrid orbitals
• The process of intermixing of orbitals to produce hybrid orbitals is called hybridization
♦ We will see a more precise definition in a later section
♦ First we need to learn more about hybrid orbitals
• Following steps from (3) to (7) will tell us the 'properties of hybrid orbitals'. They are written in 'question and answer' form:
Example 1:
• In our present case:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
• Using symbols, we write this hybridization as: (s+p+p+p)
■ So it is called a s1p3 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp3 hybridization
Example 2:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
• Using symbols, we write this hybridization as: (s+p+p)
■ So it is called a s1p2 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp2 hybridization
Example 3:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
• Using symbols, we write this hybridization as: (s+p)
■ So it is called a s1p1 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp hybridization
(i) All hybrid orbitals will be having the same shape
• If a hybrid orbital is allowed to lie on a platform, it will appear as shown in fig.4.133(a) below
(ii) Each hybrid orbital consists of two lobes
• One lobe is smaller than the other
(iii) We can draw an axis passing through the two lobes. It is shown in fig.b
(iv) The nucleus of the atom will lie near the 'point of contact' of the two lobes
• This is shown as a small red sphere in fig.b
(v) If there are two hybrid orbitals, they will appear as shown in fig.c
• The two smaller lobes are not visible because:
♦ The left smaller lobe is inside the right larger lobe
♦ The right smaller lobe is inside the left larger lobe
• Each of the two orbitals will try to push the other as far away as possible
♦ This results in the linear structure shown in fig.c
♦ We saw this feature when we discussed VSEPR theory
(vi) If there are three hybrid orbitals, they will appear as shown in fig.4.134(a) below:
• They will be at an angular distance of 120o apart
• It is a triangular shape
♦ The nucleus is placed at the center of gravity of that equilateral triangle
♦ The larger lobes are directed towards the three corners of the equilateral triangle
• So all three hybrid orbitals will lie on a plane. It is a planar (2D) structure
• Each of the three orbitals will try to push the others as far away as possible
♦ This results in the triangular structure shown in fig.a
♦ We saw this feature when we discussed VSEPR theory
(vii) If there are four hybrid orbitals, they will appear as shown in fig.4.134(b) above
• They will be at an angular distance of 109.5o apart
• It is a tetrahedral shape
• The tetrahedral shape becomes clear in fig.c
♦ The magenta dashed lines are the edges of a triangular pyramid
♦ The nucleus is placed at the center of gravity of that pyramid
♦ The larger lobes are directed towards the four corners of the pyramid
• We saw the details about tetrahedral shape when we discussed VSEPR theory. See fig.4.86 in section 4.14.
• Each of the four orbitals will try to push the others as far away as possible
♦ This results in the tetrahedral structure shown in fig.c
♦ We saw this feature when we discussed VSEPR theory
(i) Write separately, the number of each type of orbitals participating in the hybridization
(ii) Write the sum of those numbers
(iii) The ‘number of hybrid orbitals’ that will be obtained is equal to this sum
Example 1:
• In our present case, it is sp3 hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
♦ Sum of the numbers = (1+3) = 4
• So ‘number of hybrid orbitals’ obtained = 4
• That means, as a result of this hybridization, we will get four hybrid orbitals
♦ Each one of them will be known as: a sp3 hybrid orbital
• So what we see in the fig.4.134(b) is the result of sp3 hybridization
♦ Each orbital in this fig.b is a sp3 hybrid orbital
Example 2:
• The case of sp2 hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
♦ Sum of the numbers = (1+2) = 3
• So ‘number of hybrid orbitals’ obtained = 3
• That means, as a result of this hybridization, we will get three hybrid orbitals
♦ Each one of them will be known as: a sp2 hybrid orbital
• So what we see in the fig.4.134(a) is the result of sp2 hybridization
♦ Each orbital in this fig.a is a sp2 hybrid orbital
Example 3:
• The case of sp hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
♦ Sum of the numbers = (1+1) = 2
• So ‘number of hybrid orbitals’ obtained = 2
• That means, as a result of this hybridization, we will get two hybrid orbitals
♦ Each one of them will be known as: a sp hybrid orbital
• So what we see in the fig.4.133(c) is the result of sp hybridization
♦ Each orbital in this fig.c is a sp hybrid orbital
(i) All the hybrid orbitals will have the same energy value
• But it will depend on the type of hybridization
(ii) A simple procedure can be adopted:
♦ Write the 'lowest energy value' of the participating orbitals
♦ Write the 'highest energy value' of the participating orbitals
♦ The energy value of the new hybrid orbitals will lie between the two values
(iii) That means,
♦ the energy will not be lesser than the 'lowest energy value'
♦ the energy will not be greater than the 'highest energy value'
• Let us see some examples:
Example 1:
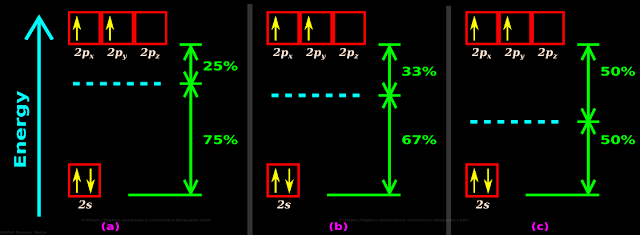
In our present case of sp3 hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the 2s orbital
♦ will be lesser than the energy of the 2p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 4, which is same as 1⁄4
✰ In percentage format, 1⁄4 is 25%
♦ The contribution of p orbitals in this hybridization is 3 in 4, which is same as 3⁄4
✰ In percentage format, 3⁄4 is 75%
(c) It is clear that each of the four sp3 hybrid orbitals will have 25% s characteristics and 75% p characteristics
(d) So the energy of each of the four sp3 hybrid orbitals will be closer to the energy value of p orbitals
• This is shown in fig.4.135(a) below. The dashed cyan line indicates the energy level of the hybrid orbitals
Example 2:
• The case of sp2 hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the s orbital
♦ will be lesser than the energy of the p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 3, which is same as 1⁄3
✰ In percentage format, 1⁄3 is approximately 33%
♦ The contribution of p orbitals in this hybridization is 2 in 3, which is same as 2⁄3
✰ In percentage format, 2⁄3 is approximately 67%
(c) It is clear that each of the four sp2 hybrid orbitals will have 33% s characteristics and 67% p characteristics
(d) So the energy of each of the three sp2 hybrid orbitals will be closer to the energy value of p orbitals
• This is shown in fig.4.135(b) above
Example 3:
• The case of sp hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the s orbital
♦ will be lesser than the energy of the p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 2, which is same as 1⁄2
✰ In percentage format, 1⁄2 is 50%
♦ The contribution of p orbitals in this hybridization is also 1 in 2, which is same as 1⁄2
✰ In percentage format, 1⁄2 is 50%
(c) It is clear that each of the two sp hybrid orbitals will have 50% s characteristics and 50% p characteristics
(d) So the energy of each of the two sp hybrid orbitals will be exactly midway between s and p orbitals
• This is shown in fig.4.135(c) above
(i) After the hybridization, the original participating orbitals will no longer exist
(ii) Other atoms will come and overlap with the new hybrid orbitals
(iii) In our present case:
• The valence shell of the C atom will no longer contain 2s and 2p orbitals
• If any other atom (like H, Cl, F, or even another C) wants to react with this C atom, they will be interacting with the four new sp3 hybrid orbitals
• Linus Pauling put forward the concept of hybridization. The basics of this concept can be explained in steps:
1. In the valence shell of the C atom, we have:
♦ One 2s orbital
✰ This is completely filled
♦ One 2px orbital
✰ This is half filled
♦ One 2py orbital
✰ This is half filled
♦ One 2pz orbital
✰ This is empty
2. So there are a total of four orbitals
• These four orbitals mix together
• The result is the formation of some new orbitals
• These new orbitals are called hybrid orbitals
• The process of intermixing of orbitals to produce hybrid orbitals is called hybridization
♦ We will see a more precise definition in a later section
♦ First we need to learn more about hybrid orbitals
• Following steps from (3) to (7) will tell us the 'properties of hybrid orbitals'. They are written in 'question and answer' form:
3. How do we name the 'different types of hybridization'?
Answer can be written with the help of three examples:Example 1:
• In our present case:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
• Using symbols, we write this hybridization as: (s+p+p+p)
■ So it is called a s1p3 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp3 hybridization
Example 2:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
• Using symbols, we write this hybridization as: (s+p+p)
■ So it is called a s1p2 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp2 hybridization
Example 3:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
• Using symbols, we write this hybridization as: (s+p)
■ So it is called a s1p1 hybridization
♦ If the superscript is ‘1’, it need not be written
■ So it is called a sp hybridization
4. We said that, as a result of hybridization, we get new orbitals called hybrid orbitals. What is the shape of those hybrid orbitals?
• Answer can be written in 7 steps:(i) All hybrid orbitals will be having the same shape
• If a hybrid orbital is allowed to lie on a platform, it will appear as shown in fig.4.133(a) below
(ii) Each hybrid orbital consists of two lobes
• One lobe is smaller than the other
(iii) We can draw an axis passing through the two lobes. It is shown in fig.b
(iv) The nucleus of the atom will lie near the 'point of contact' of the two lobes
• This is shown as a small red sphere in fig.b
 |
| Fig.4.133 |
• The two smaller lobes are not visible because:
♦ The left smaller lobe is inside the right larger lobe
♦ The right smaller lobe is inside the left larger lobe
• Each of the two orbitals will try to push the other as far away as possible
♦ This results in the linear structure shown in fig.c
♦ We saw this feature when we discussed VSEPR theory
(vi) If there are three hybrid orbitals, they will appear as shown in fig.4.134(a) below:
 |
| Fig.4.134 |
• It is a triangular shape
♦ The nucleus is placed at the center of gravity of that equilateral triangle
♦ The larger lobes are directed towards the three corners of the equilateral triangle
• So all three hybrid orbitals will lie on a plane. It is a planar (2D) structure
• Each of the three orbitals will try to push the others as far away as possible
♦ This results in the triangular structure shown in fig.a
♦ We saw this feature when we discussed VSEPR theory
(vii) If there are four hybrid orbitals, they will appear as shown in fig.4.134(b) above
• They will be at an angular distance of 109.5o apart
• It is a tetrahedral shape
• The tetrahedral shape becomes clear in fig.c
♦ The magenta dashed lines are the edges of a triangular pyramid
♦ The nucleus is placed at the center of gravity of that pyramid
♦ The larger lobes are directed towards the four corners of the pyramid
• We saw the details about tetrahedral shape when we discussed VSEPR theory. See fig.4.86 in section 4.14.
• Each of the four orbitals will try to push the others as far away as possible
♦ This results in the tetrahedral structure shown in fig.c
♦ We saw this feature when we discussed VSEPR theory
5. We saw the shape of a hybrid orbital in (4) above. How many of such hybrid orbitals will be obtained as a result of hybridization?
• Answer can be written in 3 steps:(i) Write separately, the number of each type of orbitals participating in the hybridization
(ii) Write the sum of those numbers
(iii) The ‘number of hybrid orbitals’ that will be obtained is equal to this sum
Example 1:
• In our present case, it is sp3 hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
♦ Sum of the numbers = (1+3) = 4
• So ‘number of hybrid orbitals’ obtained = 4
• That means, as a result of this hybridization, we will get four hybrid orbitals
♦ Each one of them will be known as: a sp3 hybrid orbital
• So what we see in the fig.4.134(b) is the result of sp3 hybridization
♦ Each orbital in this fig.b is a sp3 hybrid orbital
Example 2:
• The case of sp2 hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
♦ Sum of the numbers = (1+2) = 3
• So ‘number of hybrid orbitals’ obtained = 3
• That means, as a result of this hybridization, we will get three hybrid orbitals
♦ Each one of them will be known as: a sp2 hybrid orbital
• So what we see in the fig.4.134(a) is the result of sp2 hybridization
♦ Each orbital in this fig.a is a sp2 hybrid orbital
Example 3:
• The case of sp hybridization:
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
♦ Sum of the numbers = (1+1) = 2
• So ‘number of hybrid orbitals’ obtained = 2
• That means, as a result of this hybridization, we will get two hybrid orbitals
♦ Each one of them will be known as: a sp hybrid orbital
• So what we see in the fig.4.133(c) is the result of sp hybridization
♦ Each orbital in this fig.c is a sp hybrid orbital
6. What are the energies of the new hybrid orbitals
• Answer can be written in 3 steps:(i) All the hybrid orbitals will have the same energy value
• But it will depend on the type of hybridization
(ii) A simple procedure can be adopted:
♦ Write the 'lowest energy value' of the participating orbitals
♦ Write the 'highest energy value' of the participating orbitals
♦ The energy value of the new hybrid orbitals will lie between the two values
(iii) That means,
♦ the energy will not be lesser than the 'lowest energy value'
♦ the energy will not be greater than the 'highest energy value'
• Let us see some examples:
Example 1:
In our present case of sp3 hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the 2s orbital
♦ will be lesser than the energy of the 2p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 3
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 4, which is same as 1⁄4
✰ In percentage format, 1⁄4 is 25%
♦ The contribution of p orbitals in this hybridization is 3 in 4, which is same as 3⁄4
✰ In percentage format, 3⁄4 is 75%
(c) It is clear that each of the four sp3 hybrid orbitals will have 25% s characteristics and 75% p characteristics
(d) So the energy of each of the four sp3 hybrid orbitals will be closer to the energy value of p orbitals
• This is shown in fig.4.135(a) below. The dashed cyan line indicates the energy level of the hybrid orbitals
 |
| Fig.4.135 |
• The case of sp2 hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the s orbital
♦ will be lesser than the energy of the p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 2
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 3, which is same as 1⁄3
✰ In percentage format, 1⁄3 is approximately 33%
♦ The contribution of p orbitals in this hybridization is 2 in 3, which is same as 2⁄3
✰ In percentage format, 2⁄3 is approximately 67%
(c) It is clear that each of the four sp2 hybrid orbitals will have 33% s characteristics and 67% p characteristics
(d) So the energy of each of the three sp2 hybrid orbitals will be closer to the energy value of p orbitals
• This is shown in fig.4.135(b) above
Example 3:
• The case of sp hybridization:
• The energy of the new hybrid orbitals
♦ will be greater than the energy of the s orbital
♦ will be lesser than the energy of the p orbitals
• To be more precise, we can use the following 4 steps from (a) to (d):
(a) Number of participating orbitals
♦ No. of s orbitals participating in the hybridization = 1
♦ No. of p orbitals participating in the hybridization = 1
(b) We can write:
♦ The contribution of s orbital in this hybridization is 1 in 2, which is same as 1⁄2
✰ In percentage format, 1⁄2 is 50%
♦ The contribution of p orbitals in this hybridization is also 1 in 2, which is same as 1⁄2
✰ In percentage format, 1⁄2 is 50%
(c) It is clear that each of the two sp hybrid orbitals will have 50% s characteristics and 50% p characteristics
(d) So the energy of each of the two sp hybrid orbitals will be exactly midway between s and p orbitals
• This is shown in fig.4.135(c) above
7. After the hybridization, what will happen to the participating orbitals
Answer can be written in 3 steps:(i) After the hybridization, the original participating orbitals will no longer exist
(ii) Other atoms will come and overlap with the new hybrid orbitals
(iii) In our present case:
• The valence shell of the C atom will no longer contain 2s and 2p orbitals
• If any other atom (like H, Cl, F, or even another C) wants to react with this C atom, they will be interacting with the four new sp3 hybrid orbitals
• In the previous section, we saw the drawbacks in the model of the CH4 molecule
• At the beginning of the present section, we said that, Linus Pauling put forward the concept of hybridization to overcome those drawbacks
• To learn the concept of hybridization, we need to understand the properties of hybrid orbitals
• The steps (3) to (7) above help us to understand the properties of hybrid orbitals
• In the next section, we will see how actually the hybrid orbitals help to overcome the drawbacks in the CH4 model
• At the beginning of the present section, we said that, Linus Pauling put forward the concept of hybridization to overcome those drawbacks
• To learn the concept of hybridization, we need to understand the properties of hybrid orbitals
• The steps (3) to (7) above help us to understand the properties of hybrid orbitals
• In the next section, we will see how actually the hybrid orbitals help to overcome the drawbacks in the CH4 model
No comments:
Post a Comment