We are discussing the basics of VSEPR theory. In the section 4.13, we saw three examples
♦ Example 1 was related to the type AB
♦ Example 2 was related to the type AB2
♦ Example 3 was related to the type AB3
• In the previous section 4.14, we saw example 4
♦ Example 4 was related to the type AB4
• In this section, we will see the type AB5
Example 5:
1. Consider the general form of molecule: AB5
• There is one atom of element A and five atoms of element B
2. We want to know the shape of the molecule AB5
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB5 is shown in fig.4.89(a) below
♦ A is the central atom
♦ The five B atoms are distributed around A:
3. So we have 6 atoms
• Let us assume that, all the six atoms lie on the same plane
• So whatever be the positions of the atoms in AB5, the ‘molecule AB5 as a whole’ will be planar
• It will be a 2D structure
4. The VSEPR theory tells us that:
Each stick will be trying to push the other sticks as far away as possible
• In our present case, there are five sticks
♦ All the five sticks push each other with equal forces
♦ When this happens, will the sticks settle down with an angle of 72o between them?
♦ The 72o is shown in fig.4.85(b) above
5. Let us try the calculations that we did in the previous cases
For our present case, the calculations will be as follows:
(i) In AB5, there are five sticks
(ii) The central angle of a circle is 360o as shown in fig.4.89(c) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄5 = 72
(iv) This 72o is the angle between the bonds in fig.(b)
6. All sticks appear to be happy. But this is not the case. The sticks are not at all happy
■ They are not happy because, an 'alternate arrangement' is possible
• In that 'alternate arrangement', the angles between the sticks will be greater than 72o
• Naturally, the sticks will prefer that 'alternate arrangement'
• Just as in the case of the previous AB4, the 'alternate arrangement' is a 3D structure
• The following steps from (7) to (12) will help us to understand that 3D structure
7. First of all, let us try to visualize the shape in our minds. It is really simple. We can write it in (v) steps:
(i) Consider the triangular pyramid that we saw in the case of AB4
It is shown in fig.4.90(a) below:
(ii) Make an exact replica of that pyramid
• Now we have two identical triangular pyramids
(iii) Flip the second pyramid in the vertical direction
• Now we have:
♦ The first pyramid pointing upwards
♦ The second pyramid pointing downwards
✰ This is shown in fig.4.90(b)
(iv) Bring the second pyramid vertically below the first
• Now the two bases are facing each other
♦ This is shown in fig.4.90(c)
(v) Apply glue to both the bases and stick them together
• Now the two pyramids are joined together to form a new ‘type of solid’
■ This 'new type of solid' is called the trigonal bipyramid
♦ ‘bi’ stands for ’two’
♦ We indeed have two pyramids
✰ One is inverted
• This is shown in fig.4.90(d)
8. The trigonal bipyramid is the basic structure of AB5
• Next step is to find out how the total six atoms fit into that basic structure
• It can be written in (v) steps
(i) We have seen that the two base triangles are glued together
♦ So they become one single triangle
• A triangle has three corners
♦ In the fig.4.91(a) below, atoms Biii, Biv and Bv are situated at those three corners
(ii) Now two terminal atoms Bi and Bii are remaining
♦ Bi is situated at the apex of the top pyramid
♦ Bii is situated at the apex of the bottom pyramid
• This is also shown in fig.4.91(a) above
(iii) Now we have to find the position of the central atom A
• Consider the base triangle
♦ It is an equilateral triangle
• We have learned about the centroid of equilateral triangles
♦ The central atom A is situated at the centroid of the base triangle
• This is also shown in fig.4.91(a) above
• The centroid of a triangle will be equi-distant from all the three corners
♦ So The central atom A is equi-distant from Biii, Biv and Bv
• This can be represented in a '2D plane' as shown in fig.4.91(b) above
(iv) Axial atoms
• The apex of a triangular pyramid will be vertically above the 'centroid of the base'
♦ So atom Bi is vertically above A
♦ Similarly, atom Bii is vertically below A
■ Thus, Bi, A and Bii falls in the same line
■ This line is called the axis of the trigonal bipyramid
■ The atoms Bi, A and Bii are called the axial atoms
(v) Equatorial atoms
• We see that, the ‘perimeter of the base triangle’ is exact midway between Bi and Bii
■ This perimeter is called the equator of the trigonal bipyramid
■ The atoms Biii, Biv, and Bv are called equatorial atoms
9. Now we know the positions of the atoms
• Next step is to find the ‘angles between bonds’. For that, we must first learn about 'axial bonds' and 'equatorial bonds'
(i) Axial bonds:
• Consider the axis of the bipyramid
• Two bonds lie along that axis. They are:
♦ The bond between A and Bi
♦ The bond between A and Bii
■ These bonds are called axial bonds
(ii) Equatorial bonds
• Consider the base triangle
• Three bonds lie on the ‘plane of that triangle’. They are:
♦ The bond between A and Biii
♦ The bond between A and Biv
♦ The bond between A and Bv
■ These bonds are called equatorial bonds
10. In the structure of AB5, we have to learn about three types of angles. They are:
♦ The angle between any one axial bond and any one equatorial bond
♦ The angle between any two equatorial bonds
♦ The angle between the two axial bonds
✰ (We cannot say ‘any two axial bonds’. Because, there are only two axial bonds)
(i) The angle between any one axial bond and any one equatorial bond
• The axial bond lies along the axis
• The equatorial bond lies in the ‘plane of the base triangle’
• The ‘plane of the base triangle’ is perpendicular to the axis
• So this angle will be equal to 90o
• Example: ∠BiABiv = 90o
♦ This is shown in orange color in fig.4.92(a) below:
(v) The angle between any two equatorial bonds
• The equatorial bond lies in the ‘plane of the base triangle’
♦ They all start from the central atom A
• A is situated at the centroid of the base triangle
• So the equatorial bonds radiate from the 'centroid of the base' towards the corners
• So the angle between any two of these bonds will be equal to 120
• Example: ∠BiiiABv = 120o
♦ This angle is also shown in violet color in fig.4.92(a) above
Note: The earlier fig.4.91(b) also clearly shows that, the angle between any two equatorial bonds is equal to 120o
(vi) The angle between the two axial bonds
• The axial bonds lies along the axis
• The ‘axis’ is a straight line
• So the angle will be 180o
• There is only one example: ∠BiABii = 180o
♦ It is shown in white color in fig.4.92(b) above
11. So we have completely described the trigonal bipyramidal shape of AB5
• Now, there is a problem with 3D structures. We cannot draw them easily in our notebooks and records. So we adopt a different 'drawing method'. We saw it in the case of dipole moment in NH3 molecule (see fig.4.73 of section 4.11). We saw it again in the case of AB4 in the previous section
• Based on that method, let us try to represent our present AB5 molecule
• For that, first we must fix up a suitable 'plane of paper'
• This 'plane of paper' must contain the central atom A and as many terminal atoms as possible
• Such a plane is shown in fig.4.93(a) below:
We see three important points:
(i) The plane passes through A, Bi, Bii and Biv
[A plane can be made to pass through any 3 given points (Details here). So our plane can be made to pass through A, Bi and Biv. But Bi, A and Bii are on the same line. So naturally, Bii will also fall on the plane]
(ii) Biii is in front of the plane
(iii) Bv is behind the plane
(The plane is given a bit of transparency so that, Bv will also become visible)
• So our present AB5 molecule can be represented as shown in fig.4.93(b) above
12. Let us see a real life example:
• PCl5 (Phosphorus PentaChloride) has a trigonal bipyramidal structure
• It is shown in the fig.4.93 (c) above
13. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are five sticks
♦ All of them start from a common point
♦ Each stick pushes the other four, as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the trigonal bipyramidal structure
(iii) So naturally, the molecules of the form AB5 will prefer that structure
All molecules of the form AB5 will have a trigonal bipyramidal structure
• But this is not true
♦ Some AB5 molecules, which have 'lone pairs', are not exactly trigonal bipyramidal
♦ We will see them in later sections
♦ Example 1 was related to the type AB
♦ Example 2 was related to the type AB2
♦ Example 3 was related to the type AB3
• In the previous section 4.14, we saw example 4
♦ Example 4 was related to the type AB4
• In this section, we will see the type AB5
Example 5:
1. Consider the general form of molecule: AB5
• There is one atom of element A and five atoms of element B
2. We want to know the shape of the molecule AB5
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB5 is shown in fig.4.89(a) below
♦ A is the central atom
♦ The five B atoms are distributed around A:
 |
| Fig.4.89 |
• Let us assume that, all the six atoms lie on the same plane
• So whatever be the positions of the atoms in AB5, the ‘molecule AB5 as a whole’ will be planar
• It will be a 2D structure
4. The VSEPR theory tells us that:
Each stick will be trying to push the other sticks as far away as possible
• In our present case, there are five sticks
♦ All the five sticks push each other with equal forces
♦ When this happens, will the sticks settle down with an angle of 72o between them?
♦ The 72o is shown in fig.4.85(b) above
5. Let us try the calculations that we did in the previous cases
For our present case, the calculations will be as follows:
(i) In AB5, there are five sticks
(ii) The central angle of a circle is 360o as shown in fig.4.89(c) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄5 = 72
(iv) This 72o is the angle between the bonds in fig.(b)
6. All sticks appear to be happy. But this is not the case. The sticks are not at all happy
■ They are not happy because, an 'alternate arrangement' is possible
• In that 'alternate arrangement', the angles between the sticks will be greater than 72o
• Naturally, the sticks will prefer that 'alternate arrangement'
• Just as in the case of the previous AB4, the 'alternate arrangement' is a 3D structure
• The following steps from (7) to (12) will help us to understand that 3D structure
7. First of all, let us try to visualize the shape in our minds. It is really simple. We can write it in (v) steps:
(i) Consider the triangular pyramid that we saw in the case of AB4
It is shown in fig.4.90(a) below:
 |
| Fig.4.90 |
• Now we have two identical triangular pyramids
(iii) Flip the second pyramid in the vertical direction
• Now we have:
♦ The first pyramid pointing upwards
♦ The second pyramid pointing downwards
✰ This is shown in fig.4.90(b)
(iv) Bring the second pyramid vertically below the first
• Now the two bases are facing each other
♦ This is shown in fig.4.90(c)
(v) Apply glue to both the bases and stick them together
• Now the two pyramids are joined together to form a new ‘type of solid’
■ This 'new type of solid' is called the trigonal bipyramid
♦ ‘bi’ stands for ’two’
♦ We indeed have two pyramids
✰ One is inverted
• This is shown in fig.4.90(d)
8. The trigonal bipyramid is the basic structure of AB5
• Next step is to find out how the total six atoms fit into that basic structure
• It can be written in (v) steps
(i) We have seen that the two base triangles are glued together
♦ So they become one single triangle
• A triangle has three corners
♦ In the fig.4.91(a) below, atoms Biii, Biv and Bv are situated at those three corners
 |
| Fig.4.91 |
♦ Bi is situated at the apex of the top pyramid
♦ Bii is situated at the apex of the bottom pyramid
• This is also shown in fig.4.91(a) above
(iii) Now we have to find the position of the central atom A
• Consider the base triangle
♦ It is an equilateral triangle
• We have learned about the centroid of equilateral triangles
♦ The central atom A is situated at the centroid of the base triangle
• This is also shown in fig.4.91(a) above
• The centroid of a triangle will be equi-distant from all the three corners
♦ So The central atom A is equi-distant from Biii, Biv and Bv
• This can be represented in a '2D plane' as shown in fig.4.91(b) above
(iv) Axial atoms
• The apex of a triangular pyramid will be vertically above the 'centroid of the base'
♦ So atom Bi is vertically above A
♦ Similarly, atom Bii is vertically below A
■ Thus, Bi, A and Bii falls in the same line
■ This line is called the axis of the trigonal bipyramid
■ The atoms Bi, A and Bii are called the axial atoms
(v) Equatorial atoms
• We see that, the ‘perimeter of the base triangle’ is exact midway between Bi and Bii
■ This perimeter is called the equator of the trigonal bipyramid
■ The atoms Biii, Biv, and Bv are called equatorial atoms
9. Now we know the positions of the atoms
• Next step is to find the ‘angles between bonds’. For that, we must first learn about 'axial bonds' and 'equatorial bonds'
(i) Axial bonds:
• Consider the axis of the bipyramid
• Two bonds lie along that axis. They are:
♦ The bond between A and Bi
♦ The bond between A and Bii
■ These bonds are called axial bonds
(ii) Equatorial bonds
• Consider the base triangle
• Three bonds lie on the ‘plane of that triangle’. They are:
♦ The bond between A and Biii
♦ The bond between A and Biv
♦ The bond between A and Bv
■ These bonds are called equatorial bonds
10. In the structure of AB5, we have to learn about three types of angles. They are:
♦ The angle between any one axial bond and any one equatorial bond
♦ The angle between any two equatorial bonds
♦ The angle between the two axial bonds
✰ (We cannot say ‘any two axial bonds’. Because, there are only two axial bonds)
(i) The angle between any one axial bond and any one equatorial bond
• The axial bond lies along the axis
• The equatorial bond lies in the ‘plane of the base triangle’
• The ‘plane of the base triangle’ is perpendicular to the axis
• So this angle will be equal to 90o
• Example: ∠BiABiv = 90o
♦ This is shown in orange color in fig.4.92(a) below:
 |
| Fig.4.92 |
• The equatorial bond lies in the ‘plane of the base triangle’
♦ They all start from the central atom A
• A is situated at the centroid of the base triangle
• So the equatorial bonds radiate from the 'centroid of the base' towards the corners
• So the angle between any two of these bonds will be equal to 120
• Example: ∠BiiiABv = 120o
♦ This angle is also shown in violet color in fig.4.92(a) above
Note: The earlier fig.4.91(b) also clearly shows that, the angle between any two equatorial bonds is equal to 120o
(vi) The angle between the two axial bonds
• The axial bonds lies along the axis
• The ‘axis’ is a straight line
• So the angle will be 180o
• There is only one example: ∠BiABii = 180o
♦ It is shown in white color in fig.4.92(b) above
11. So we have completely described the trigonal bipyramidal shape of AB5
• Now, there is a problem with 3D structures. We cannot draw them easily in our notebooks and records. So we adopt a different 'drawing method'. We saw it in the case of dipole moment in NH3 molecule (see fig.4.73 of section 4.11). We saw it again in the case of AB4 in the previous section
• Based on that method, let us try to represent our present AB5 molecule
• For that, first we must fix up a suitable 'plane of paper'
• This 'plane of paper' must contain the central atom A and as many terminal atoms as possible
• Such a plane is shown in fig.4.93(a) below:
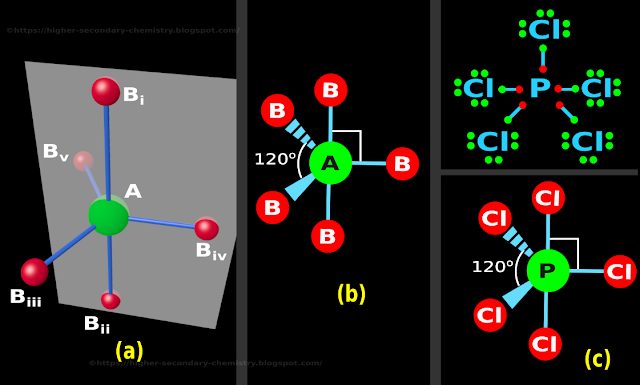 |
| Fig.4.93 |
(i) The plane passes through A, Bi, Bii and Biv
[A plane can be made to pass through any 3 given points (Details here). So our plane can be made to pass through A, Bi and Biv. But Bi, A and Bii are on the same line. So naturally, Bii will also fall on the plane]
(ii) Biii is in front of the plane
(iii) Bv is behind the plane
(The plane is given a bit of transparency so that, Bv will also become visible)
• So our present AB5 molecule can be represented as shown in fig.4.93(b) above
12. Let us see a real life example:
• PCl5 (Phosphorus PentaChloride) has a trigonal bipyramidal structure
• It is shown in the fig.4.93 (c) above
13. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are five sticks
♦ All of them start from a common point
♦ Each stick pushes the other four, as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the trigonal bipyramidal structure
(iii) So naturally, the molecules of the form AB5 will prefer that structure
• Based on the above discussion, we are inclined to think that:
• But this is not true
♦ Some AB5 molecules, which have 'lone pairs', are not exactly trigonal bipyramidal
♦ We will see them in later sections
• Now we continue the discussion on examples which do not have lone pairs
• The next example is of the type: AB6
• We will see it in the next section
• The next example is of the type: AB6
• We will see it in the next section
No comments:
Post a Comment