In the previous section, we completed a discussion on partial covalent character in ionic bonds. In this section, we will see VSEPR theory
■ 'VSEPR theory' is the short form of:
Valence Shell Electron Pair Repulsion theory
• Let us arrange the words in the above sentence, into groups. This is shown below:
• This 'grouping' gives us a basic idea. It can be written in 3 steps:
(i) The theory deals with a 'repulsion'
♦ This is marked in green color
(ii) But 'repulsion' between what?
• The repulsion is between 'electron pairs'
♦ This is marked in yellow color
(iii) But which 'electron pairs'?
• Those electron pairs, which are situated in the valence shells
♦ This is marked by the green color
■ So we have to consider the 'electron pairs' in the 'valence shells'
■ Note that, the 'repulsion' is between 'pairs of electrons'. Not between individual electrons. We do not consider the repulsion between two electrons within a pair
■ We will analyze some examples. By doing so, we will learn some basic features of the theory
Example 1:
1. Consider a general form of molecule: AB
• There is one atom of element A and one atom of element B
2. We want to know the shape of the molecule AB
• Let us assume that, the bond between A and B is ‘covalent’
3. Then the shape is obvious. We can write it in steps:
(i) We can draw a line between any two points in space
♦ So the shape of AB will be ‘linear’
(ii) We can keep A stationary and move B to any position
♦ The shape of AB will be linear all the while
3. So there is not much to worry about the shape of molecules of the type AB
• It will be a linear structure, with a covalent bond (single, double or triple) between A and B
• HCl, O2, N2, etc., are of this type
Example 2:
1. Consider another general form of molecule: AB2
• There is one atom of element A and two atoms of element B
2. We want to know the shape of the molecule AB2
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB2 is shown in fig.4.80(a) below
♦ A is the central atom
♦ The two B atoms are distributed on either sides of A:
3. So we have 3 atoms
• There is always a plane which passes through any three given points in space
• So whatever be the positions of the atoms in AB2, the ‘molecule AB2 as a whole’ will be planar
• It will be a 2D structure
■ Thus we can write:
All the atoms in AB2 will lie on the same plane
4. But even while lying on the same plane, there are different possibilities:
• They are shown in figs.4.80 (b), (c) and (d)
♦ In fig.b, the angle between the two bonds is acute
♦ In fig.c, the angle between the two bonds is 90o
♦ In fig.d, the angle between the two bonds is obtuse
5. We want to know the exact angle
■ The VSEPR theory can help us in this situation
• This can be explained in 4 steps
(i) We know that, in the ball-and-stick model, each stick will contain two electrons
♦ Since the number of electrons is ‘two’, we can call them a ‘pair’
♦ So in the ball-and-stick model, each stick will represent a pair of electrons
(ii) We know that, electrons repel each other. So the sticks will repel each other
• The VSEPR theory tells us this:
♦ Consider any one stick
♦ That stick will be trying to push the other sticks as far away as possible
♦ Each of the other sticks will also be doing the same
(iii) Based on this, we can write:
♦ The arrangement in fig.4.80(b) is not possible because, the sticks are too close to each other
♦ In fig.4.80(c), the sticks are further apart. But still more ‘separation’ is possible
♦ More separation can be achieved by making the angle obtuse. This is shown in fig.d
♦ But even more separation is possible by increasing the obtuse angle
(iv) The maximum separation is achieved when the obtuse angle is increased to 180o
• This is shown in fig.4.81(a) below:
• Further increase beyond 180o is not possible. Because, then the angle on the bottom side will become less than 180o. This is shown in fig.4.81(b)
6. So fig.4.81(a) shows the final structure of AB2
• We see that, all atoms of AB2 fall in a line
■ So it is called linear structure
7. We note an interesting point here. It can be written in 4 steps:
(i) In AB2, there are two sticks
(ii) The central angle of a circle is 360o as shown in fig.4.81(c) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄2 = 180
(iv) This 180o is the angle between the bonds
8. Let us see some real life examples:
• BeH2 (Beryllium Hydride), CO2 (Carbon dioxide) and HCN (Hydrogen cyanide) are of the form AB2
• They all have linear structures
• They are shown in the fig.4.82 below:
• Note that, there are two double bonds in CO2
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
• Also note that, there is a triple bond in HCN
♦ But in VSEPR theory,
✰ a triple bond is also considered as a 'single stick'
9. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are two sticks
♦ Both of them start from a common point
♦ Each stick pushes the other as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the linear structure
(iii) So naturally, the molecules of the form AB2 will prefer that structure
All molecules of the form AB2 will have a linear structure
• But this is not true
♦ Some AB2 molecules, which have 'lone pairs', are seen in bent structures
♦ We will see them in later sections
Each stick will be trying to push the other sticks as far away as possible
• In our present case, there are three sticks
♦ All the three sticks push each other with equal forces
♦ When this happens, the sticks will settle down with an angle of 120o between them
♦ This is shown in fig.4.83(b) above
5. Note that, all four atoms lie on the same plane
• The 'angle of 120o' is the only option available
• If any of the three angles is changed to another value, pushing other sticks 'as far away as possible' will not be achieved
6. Now let us join the three terminal atoms with 'imaginary lines'
• Since they are imaginary lines, we will use dashed lines
♦ They are shown in magenta color in fig.4.83(c) above
• We see that, the three magenta dashed lines together give a triangle
■ So, this structure with the three sticks at 120o apart, is called trigonal planar structure
7. We note an interesting point here. It can be written in 4 steps:
(i) In AB3, there are three sticks
(ii) The central angle of a circle is 360o as shown in fig.4.83(d) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄3 = 120
(iv) This 120o is the angle between the bonds
■ Ceiling fans with three leaves make use of this angle. When the three leaves are 120o apart, a 'uniform distribution' of leaves is achieved around the axis
8. Let us see some real life examples:
• BH3 (Boron Hydride), H2CO (Formaldehyde) and CO32- (Carbonate ion) have trigonal planar structures
• They are shown in the fig.4.84 below:
• Note that, there is a double bond each in H2CO and CO32-
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
9. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are three sticks
♦ All of them start from a common point
♦ Each stick pushes the other two as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the trigonal planar structure
(iii) So naturally, the molecules of the form AB3 will prefer that structure
All molecules of the form AB3 will have a trigonal planar structure
• But this is not true
♦ Some AB3 molecules, which have 'lone pairs', are not planar
♦ We will see them in later sections
■ 'VSEPR theory' is the short form of:
Valence Shell Electron Pair Repulsion theory
• Let us arrange the words in the above sentence, into groups. This is shown below:
• This 'grouping' gives us a basic idea. It can be written in 3 steps:
(i) The theory deals with a 'repulsion'
♦ This is marked in green color
(ii) But 'repulsion' between what?
• The repulsion is between 'electron pairs'
♦ This is marked in yellow color
(iii) But which 'electron pairs'?
• Those electron pairs, which are situated in the valence shells
♦ This is marked by the green color
■ So we have to consider the 'electron pairs' in the 'valence shells'
■ Note that, the 'repulsion' is between 'pairs of electrons'. Not between individual electrons. We do not consider the repulsion between two electrons within a pair
■ We will analyze some examples. By doing so, we will learn some basic features of the theory
Example 1:
1. Consider a general form of molecule: AB
• There is one atom of element A and one atom of element B
2. We want to know the shape of the molecule AB
• Let us assume that, the bond between A and B is ‘covalent’
3. Then the shape is obvious. We can write it in steps:
(i) We can draw a line between any two points in space
♦ So the shape of AB will be ‘linear’
(ii) We can keep A stationary and move B to any position
♦ The shape of AB will be linear all the while
3. So there is not much to worry about the shape of molecules of the type AB
• It will be a linear structure, with a covalent bond (single, double or triple) between A and B
• HCl, O2, N2, etc., are of this type
Example 2:
1. Consider another general form of molecule: AB2
• There is one atom of element A and two atoms of element B
2. We want to know the shape of the molecule AB2
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB2 is shown in fig.4.80(a) below
♦ A is the central atom
♦ The two B atoms are distributed on either sides of A:
 |
| Fig.4.80 |
• There is always a plane which passes through any three given points in space
• So whatever be the positions of the atoms in AB2, the ‘molecule AB2 as a whole’ will be planar
• It will be a 2D structure
■ Thus we can write:
All the atoms in AB2 will lie on the same plane
4. But even while lying on the same plane, there are different possibilities:
• They are shown in figs.4.80 (b), (c) and (d)
♦ In fig.b, the angle between the two bonds is acute
♦ In fig.c, the angle between the two bonds is 90o
♦ In fig.d, the angle between the two bonds is obtuse
5. We want to know the exact angle
■ The VSEPR theory can help us in this situation
• This can be explained in 4 steps
(i) We know that, in the ball-and-stick model, each stick will contain two electrons
♦ Since the number of electrons is ‘two’, we can call them a ‘pair’
♦ So in the ball-and-stick model, each stick will represent a pair of electrons
(ii) We know that, electrons repel each other. So the sticks will repel each other
• The VSEPR theory tells us this:
♦ Consider any one stick
♦ That stick will be trying to push the other sticks as far away as possible
♦ Each of the other sticks will also be doing the same
(iii) Based on this, we can write:
♦ The arrangement in fig.4.80(b) is not possible because, the sticks are too close to each other
♦ In fig.4.80(c), the sticks are further apart. But still more ‘separation’ is possible
♦ More separation can be achieved by making the angle obtuse. This is shown in fig.d
♦ But even more separation is possible by increasing the obtuse angle
(iv) The maximum separation is achieved when the obtuse angle is increased to 180o
• This is shown in fig.4.81(a) below:
 |
| Fig.4.81 |
6. So fig.4.81(a) shows the final structure of AB2
• We see that, all atoms of AB2 fall in a line
■ So it is called linear structure
7. We note an interesting point here. It can be written in 4 steps:
(i) In AB2, there are two sticks
(ii) The central angle of a circle is 360o as shown in fig.4.81(c) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄2 = 180
(iv) This 180o is the angle between the bonds
8. Let us see some real life examples:
• BeH2 (Beryllium Hydride), CO2 (Carbon dioxide) and HCN (Hydrogen cyanide) are of the form AB2
• They all have linear structures
• They are shown in the fig.4.82 below:
 |
| Fig.4.82 |
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
• Also note that, there is a triple bond in HCN
♦ But in VSEPR theory,
✰ a triple bond is also considered as a 'single stick'
9. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are two sticks
♦ Both of them start from a common point
♦ Each stick pushes the other as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the linear structure
(iii) So naturally, the molecules of the form AB2 will prefer that structure
• Based on the above discussion, we are inclined to think that:
• But this is not true
♦ Some AB2 molecules, which have 'lone pairs', are seen in bent structures
♦ We will see them in later sections
Now we continue the discussion on examples which do not have lone pairs
Example 3:
1. Consider another general form of molecule: AB3
• There is one atom of element A and three atoms of element B
2. We want to know the shape of the molecule AB3
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB3 is shown in fig.4.83(a) below
♦ A is the central atom
♦ The three B atoms are distributed around A:
3. So we have 4 atoms
• There is always a plane which passes through any three given points in space
• If we are lucky, a fourth given point will also lie on that same plane
• In our present case, let us assume that, the fourth point also lies on the same plane
• So in our present case, all the four atoms lie on the same plane
• So whatever be the positions of the atoms in AB3, the ‘molecule AB3 as a whole’ will be planar
• It will be a 2D structure
■ Thus we can write:
All the atoms in AB3 will lie on the same plane
4. The VSEPR theory tells us that:
Example 3:
1. Consider another general form of molecule: AB3
• There is one atom of element A and three atoms of element B
2. We want to know the shape of the molecule AB3
• Let us assume that, the bonds are ‘covalent’
• A ball-and-stick model of AB3 is shown in fig.4.83(a) below
♦ A is the central atom
♦ The three B atoms are distributed around A:
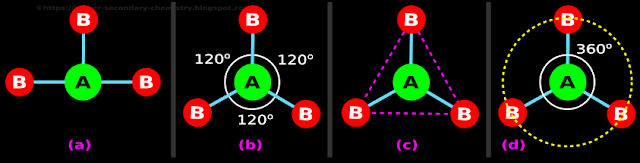 |
| Fig.4.83 |
• There is always a plane which passes through any three given points in space
• If we are lucky, a fourth given point will also lie on that same plane
• In our present case, let us assume that, the fourth point also lies on the same plane
• So in our present case, all the four atoms lie on the same plane
• So whatever be the positions of the atoms in AB3, the ‘molecule AB3 as a whole’ will be planar
• It will be a 2D structure
■ Thus we can write:
All the atoms in AB3 will lie on the same plane
4. The VSEPR theory tells us that:
• In our present case, there are three sticks
♦ All the three sticks push each other with equal forces
♦ When this happens, the sticks will settle down with an angle of 120o between them
♦ This is shown in fig.4.83(b) above
5. Note that, all four atoms lie on the same plane
• The 'angle of 120o' is the only option available
• If any of the three angles is changed to another value, pushing other sticks 'as far away as possible' will not be achieved
6. Now let us join the three terminal atoms with 'imaginary lines'
• Since they are imaginary lines, we will use dashed lines
♦ They are shown in magenta color in fig.4.83(c) above
• We see that, the three magenta dashed lines together give a triangle
■ So, this structure with the three sticks at 120o apart, is called trigonal planar structure
7. We note an interesting point here. It can be written in 4 steps:
(i) In AB3, there are three sticks
(ii) The central angle of a circle is 360o as shown in fig.4.83(d) above
(iii) We divide this 360o by the 'number of sticks'
♦ We get: 360⁄3 = 120
(iv) This 120o is the angle between the bonds
■ Ceiling fans with three leaves make use of this angle. When the three leaves are 120o apart, a 'uniform distribution' of leaves is achieved around the axis
8. Let us see some real life examples:
• BH3 (Boron Hydride), H2CO (Formaldehyde) and CO32- (Carbonate ion) have trigonal planar structures
• They are shown in the fig.4.84 below:
 |
| Fig.4.84 |
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
9. We will now write a basic concept that we must all keep in our minds. It can be written in 3 steps:
(i) We want a structure which satisfies the following three conditions:
♦ There are three sticks
♦ All of them start from a common point
♦ Each stick pushes the other two as far away as possible
(ii) There is only one structure in the whole universe that can satisfy all the above three conditions:
♦ It is the trigonal planar structure
(iii) So naturally, the molecules of the form AB3 will prefer that structure
• Based on the above discussion, we are inclined to think that:
• But this is not true
♦ Some AB3 molecules, which have 'lone pairs', are not planar
♦ We will see them in later sections
• Now we continue the discussion on examples which do not have lone pairs
• The next example is of the type: AB4
• We will see it in the next section
• The next example is of the type: AB4
• We will see it in the next section
No comments:
Post a Comment