We want to learn about the Bohr model of atom. For that, we had to first learn about 'wave nature' and 'particle nature' of electromagnetic radiations. In this regard,
• In section 2.5, we saw the 'wave nature of the electromagnetic radiations' and the 'electromagnetic spectrum'
• In section 2.6, we saw how 'particle nature' came to be known to the scientific community
• In the section 2.7, we saw how Albert Einstein proved the 'particle nature'. We also saw that the 'concept of dual nature' was accepted by the scientific community
■ The next step is to learn about Quantization. In this regard,
• In the previous section 2.8, we saw the basics about atomic spectrum
• We want to know why only certain 'quantities of energy' are suitable for absorption
• In this section, we will discuss it by considering the 'electron of hydrogen' as an example
1. Consider a sample of hydrogen gas (at low pressure) in a glass tube sealed at both ends
• Pass an electric discharge through it
2. The H2 molecules will dissociate into H atoms
• The electrons in the atoms absorb energy and get promoted to higher energy levels
3. These ‘excited electrons’ come back to their ‘ground state’ by giving off energies
• These ‘given off energies’appear as ‘radiations emitted from H atoms’
4. These emitted radiations are allowed to pass through a prism
• Thus the components get separated from each other
5. These separated components are allowed to fall on a photographic plate
• Thus we get a ‘hard copy’ of the emission spectrum
• This 'hard copy' is shown in fig.2.23 below:
6. We see four lines:
• A reddish line, a greenish blue line, an indigo line and a violet line
7. Why only ‘lines’?
• Why not ‘regions’?
• Why so much gap between the reddish and greenish blue lines?
8. Niels Bohr would find the answers in 1913
• But the emission spectrum shown in fig.2.23 was obtained even before 1885
• So it is clear that, scientists were trying to find the answers for many years
• Let us first see the 'developments which took place between 1885 and 1913'
9. On the basis of scientific observations, Johann Balmer gave the following expression in 1885:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{2^2}-\frac{1}{n^2}\right)}$
Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 3 (ie., n = 3, 4, 5, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
10. What is the significance of this expression? What happens when we put the various values for n?
• Let us first put n = 3
• We get: $\mathbf\small{\bar{\nu}_{(n=3)}=109677\left(\frac{1}{2^2}-\frac{1}{3^2}\right)}$ = 15232.9167 cm-1
⇒ $\mathbf\small{\lambda_{(n=3)}=\frac{1}{\bar{\nu}_{(n=3)}}=\frac{1}{15232.9167}=6.5647\times10^{-5}}$ cm
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 6.5647 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 656.47 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 656.47 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 620-750 nm
• We have seen that there is no clear cut boundaries between the colors in the visible spectrum
♦ There is a slow gradation from one color to another
♦ Towards '750 nm', there will be more redness
♦ Towards '620 nm', there will be more yellowness
(ii) The value we obtained using the expression given by Balmer is 656.47 nm
• It falls within the range 620-750 nm
• '656.47 nm' will have the influence of red, orange and yellow
• This is the color of the right most reddish line in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 656.47 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the emission spectrum
11. Let us put n = 4
• We get: $\mathbf\small{\bar{\nu}_{(n=4)}=109677\left(\frac{1}{2^2}-\frac{1}{4^2}\right)}$ = 20564.4375 cm-1
⇒ $\mathbf\small{\lambda_{(n=4)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{20564.4375}=4.8628\times10^{-5}}$ cm
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 4.8628 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 486.28 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 486.28 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
♦ This is the range of blue light
• Consider the wavelength range: 495-570 nm
♦ This is the range of green light
(ii) The value we obtained using the equation given by Balmer is 486.28 nm
• It falls within the range 450-495 nm
• So it must be blue light
♦ But note that, 486.28 is close to 495, which is the boundary between blue and green
♦ We know that, there is no clear cut boundary lines between the colors in the visible spectrum
♦ There is a gradual gradation from one color to another
♦ So 486.28 is mostly blue, with some influence of green
• It is clear that, 486.28 nm is the wavelength of the greenish blue line (second from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 486.28 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the second line from the right in the emission spectrum
12. Let us put n = 5
• Following the same procedure as above, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 434.17 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 450-425 nm
• This is the range of indigo light
• That is., if any radiation have a wavelength between 450 and 425 nm, it would be an indigo light
(ii) The value we obtained using the equation given by Balmer is 434.17 nm
• It falls within the range 450-425 nm
• So it is indigo light
• This is the wavelength corresponding to the indigo line (third line from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 434.17 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the third line from the right in the emission spectrum
13. Let us put n = 6
• We get: $\mathbf\small{\lambda_{(n=6)}}$ = 410.29 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 425-380 nm
• This is the range of violet light
(ii) The value we obtained using the equation given by Balmer is 410.29 nm
• It falls within the range 425-380 nm
• So it is violet light
• This is the wavelength corresponding to the violet line (fourth line from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 410.29 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the fourth line from the right in the emission spectrum
14. Since the wavelength corresponding to each line is known, we can plot them on our familiar graph. This is shown in fig.2.24 below:
• We see that, all the four lines fall well within the range of 380-750 nm
• 380-750 nm is the range of visible light
■ So we can write:
All lines given by Balmer's expression, fall within the visible range of the electromagnetic spectrum
1. The data available to Balmer was these:
(i) A reddish line occurs at the point 656.47 on the graph
(ii) A greenish blue line occurs at the point 486.28 on the graph
(iii) An indigo line occurs at the point 434.17 on the graph
(iv) A violet line occurs at the point 410.29 on the graph
2. After analyzing the above data, Balmer discovered the mathematical relation between the points
• This relation is the expression that we saw in (9) above
• So Balmer gave a 'mathematical relation'. He did not say any thing about the 'structure of the atom'
• We too can derive the same expression if we have a sound knowledge in advanced mathematics. All we would need is the data in (1). We would not need to know the 'structure of atom'
3. However, Balmer's expression helped Niels Bohr very much in his research works
• Also, the lines in fig.2.23 are considered together as a set, and is given the name: Balmer Series
• Luckily for us, they were in the visible region of the electromagnetic spectrum. So we were able to see them
■ Do the hydrogen atoms emit invisible radiations?
• They certainly do
• Hard copy of such radiations can be obtained in special photographic plates
• We must analyze those invisible radiations too
1. Like the Balmer series, there is another ‘series of lines’ to the left of the violet color
• This series is called the Lyman series
• It was discovered by Theodore Lyman
2. Since they have wavelengths less than violet, the radiations corresponding to those lines will be invisible
• The hard copy obtained in special photographic plate is shown in fig.2.25 below:
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{1^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 2 (ie., n = 2, 3, 4, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 12
(ii) The least possible value of ‘n’ has changed from 3 to 2
5. Let us first put n = 2
• We get: $\mathbf\small{\bar{\nu}_{(n=2)}=109677\left(\frac{1}{1^2}-\frac{1}{2^2}\right)}$ = 82257.75 cm-1
⇒ $\mathbf\small{\lambda_{(n=2)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{82257.75}}$ = 1.2157 × 10-5 cm
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 1.2157 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 121.57 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 121.57 nm
• So, using the expression for Lyman series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.25?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 10-400 nm
This is the range corresponding to ultraviolet radiations
(ii) The value we obtained using the expression for Lyman series is 121.57 nm
• It falls within the range 10-400 nm
• So 121.57 nm is the wavelength corresponding to the right most line in Lyman series in fig.2.24
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 121.57 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Lyman series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Lyman series
For n = 3, we get: $\mathbf\small{\lambda_{(n=3)}}$ = 102.57 nm
♦ The second line from the right in the Lyman series corresponds to this wavelength
For n = 4, we get: $\mathbf\small{\lambda_{(n=4)}}$ = 97.26 nm
♦ The third line from the right in the Lyman series corresponds to this wavelength
For n = 5, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 94.98 nm
♦ The fourth line from the right in the Lyman series corresponds to this wavelength
All these wavelengths fall within the range 10-400 nm
7. So we can write:
The Lyman series falls in the ultra violet region of the electromagnetic spectrum
• This series falls to the right of the red color
• This series is called the Paschen series
• It was discovered by Friedrich Paschen
2. Since they have wavelengths greater than red, the radiations corresponding to those lines will be invisible
The hard copy obtained in special photographic plate is shown in fig.2.26 below:
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{3^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 3 (ie., n = 4, 5, 6, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 32
(ii) The least possible value of ‘n’ has changed from 3 to 4
5. Let us first put n = 4
• We get: $\mathbf\small{\bar{\nu}_{(n=4)}=109677\left(\frac{1}{3^2}-\frac{1}{4^2}\right)}$ = 5331.520 cm-1
⇒ $\mathbf\small{\lambda_{(n=4)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{5331.520}}$ = 1.87564 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1.87564 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1875.64 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1875.64 nm
• So, using the expression for Paschen series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.26?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Paschen series is 1875.64 nm
• It falls within the range 750 nm - 106 nm
• So 1875.64 nm is the wavelength corresponding to the right most line in Paschen series in fig.2.25
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 1875.64 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Paschen series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Paschen series
For n = 5, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 1282.17 nm
♦ The second line from the right in the Paschen series corresponds to this wavelength
For n = 6, we get: $\mathbf\small{\lambda_{(n=6)}}$ = 1094.12 nm
♦ The third line from the right in the Paschen series corresponds to this wavelength
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 1005.22 nm
♦ The fourth line from the right in the Paschen series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Paschen series falls in the infrared region of the electromagnetic spectrum
• This series is called the Brackett series
• It was discovered by Frederick Sumner Brackett
2. These lines also correspond to invisible radiations
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{4^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 5 (ie., n = 5, 6, 7, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 42
(ii) The least possible value of ‘n’ has changed from 3 to 5
5. Let us first put n = 5
• We get: $\mathbf\small{\bar{\nu}_{(n=5)}=109677\left(\frac{1}{4^2}-\frac{1}{5^2}\right)}$ = 2467.7325 cm-1
⇒ $\mathbf\small{\lambda_{(n=5)}=\frac{1}{\bar{\nu}_{(n=5)}}=\frac{1}{2467.7325}}$ = 4.0523 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4.0523 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4052.3 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4052.3 nm
• So, using the expression for Brackett series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Paschen series is 4052.3 nm
• It falls within the range 750 nm - 106 nm
• So 4052.3 nm is the wavelength corresponding to the right most line in Brackett series
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 4052.3 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Brackett series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Brackett series
For n = 6, we get: $\mathbf\small{\lambda_{(n=6)}}$ = 2625.89 nm
♦ The second line from the right in the Brackett series corresponds to this wavelength
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 2166.14 nm
♦ The third line from the right in the Brackett series corresponds to this wavelength
For n = 8, we get: $\mathbf\small{\lambda_{(n=8)}}$ = 1945.11 nm
♦ The fourth line from the right in the Brackett series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Brackett series falls in the infrared region of the electromagnetic spectrum
• This series is called the Pfund series
• It was discovered by August Herman Pfund
2. These lines also correspond to invisible radiations
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{5^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 6 (ie., n = 6, 7, 8, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 52
(ii) The least possible value of ‘n’ has changed from 3 to 6
5. Let us first put n = 6
• We get: $\mathbf\small{\bar{\nu}_{(n=6)}=109677\left(\frac{1}{5^2}-\frac{1}{6^2}\right)}$ = 1340.49667 cm-1
⇒ $\mathbf\small{\lambda_{(n=6)}=\frac{1}{\bar{\nu}_{(n=6)}}=\frac{1}{1340.49667}}$ = 7.45992 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7.45992 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7459.92 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7459.92 nm
• So, using the expression for Pfund series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Pfund series is 7459.92 nm
• It falls within the range 750 nm - 106 nm
• So 4052.3 nm is the wavelength corresponding to the right most line in Pfund series
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 7459.92 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Pfund series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Pfund series
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 4653.82 nm
♦ The second line from the right in the Pfund series corresponds to this wavelength
For n = 8, we get: $\mathbf\small{\lambda_{(n=8)}}$ = 3740.59 nm
♦ The third line from the right in the Pfund series corresponds to this wavelength
For n = 9, we get: $\mathbf\small{\lambda_{(n=9)}}$ = 3297.02 nm
♦ The fourth line from the right in the Pfund series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Pfund series falls in the infrared region of the electromagnetic spectrum
• Consider the expression for each series that we saw above
• We see that, there is a regular pattern
• Because of the regular pattern, a ‘general expression’ can be derived
• This ‘general expression’ will represent all the expressions. It is given below:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n1 is an integer equal to or greater than 1 (ie., n1 = 1, 2, 3, . . .)
♦ n2 is equal to [(n1+1), (n1+2), (n1+3), . . . ]
♦ Note that, ‘n1’ has to be an integer. It cannot be a fraction or decimal
♦ When ‘n1’ is an integer, n2 will naturally become an integer
■ In the general expression,
♦ when we put n1 = 1, we get the Lyman series
♦ when we put n1 = 2, we get the Balmer series
♦ when we put n1 = 3, we get the Paschen series
♦ so on . . .
■ This general expression was derived by Swedish spectroscopist Johannes Rydberg
• He derived this expression independently. That is., he did not have any knowledge about the discoveries made by Lyman, Balmer, Paschen, Brackett and Pfund
■ So we can write:
• Lyman, Balmer, Paschen, Brackett and Pfund discovered the various series
• Rydberg independently discovered the expression which can represent any series in the hydrogen spectrum
• The value '109677 cm-1' is named as Rydberg constant for Hydrogen in his honor
■ Let us find the unit of '109677':
♦ In the general expression, we have $\mathbf\small{\bar{\nu}}$ on the left side
♦ The unit of $\mathbf\small{\bar{\nu}}$ is cm-1
♦ On the right side, the 'quantities within brackets' are numbers. They do not have any units
♦ So the unit of '109677' is cm-1.
• In section 2.5, we saw the 'wave nature of the electromagnetic radiations' and the 'electromagnetic spectrum'
• In section 2.6, we saw how 'particle nature' came to be known to the scientific community
• In the section 2.7, we saw how Albert Einstein proved the 'particle nature'. We also saw that the 'concept of dual nature' was accepted by the scientific community
■ The next step is to learn about Quantization. In this regard,
• In the previous section 2.8, we saw the basics about atomic spectrum
• We want to know why only certain 'quantities of energy' are suitable for absorption
• In this section, we will discuss it by considering the 'electron of hydrogen' as an example
1. Consider a sample of hydrogen gas (at low pressure) in a glass tube sealed at both ends
• Pass an electric discharge through it
2. The H2 molecules will dissociate into H atoms
• The electrons in the atoms absorb energy and get promoted to higher energy levels
3. These ‘excited electrons’ come back to their ‘ground state’ by giving off energies
• These ‘given off energies’appear as ‘radiations emitted from H atoms’
4. These emitted radiations are allowed to pass through a prism
• Thus the components get separated from each other
5. These separated components are allowed to fall on a photographic plate
• Thus we get a ‘hard copy’ of the emission spectrum
• This 'hard copy' is shown in fig.2.23 below:
 |
| Fig.2.23 |
• A reddish line, a greenish blue line, an indigo line and a violet line
7. Why only ‘lines’?
• Why not ‘regions’?
• Why so much gap between the reddish and greenish blue lines?
8. Niels Bohr would find the answers in 1913
• But the emission spectrum shown in fig.2.23 was obtained even before 1885
• So it is clear that, scientists were trying to find the answers for many years
• Let us first see the 'developments which took place between 1885 and 1913'
9. On the basis of scientific observations, Johann Balmer gave the following expression in 1885:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{2^2}-\frac{1}{n^2}\right)}$
Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 3 (ie., n = 3, 4, 5, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
10. What is the significance of this expression? What happens when we put the various values for n?
• Let us first put n = 3
• We get: $\mathbf\small{\bar{\nu}_{(n=3)}=109677\left(\frac{1}{2^2}-\frac{1}{3^2}\right)}$ = 15232.9167 cm-1
⇒ $\mathbf\small{\lambda_{(n=3)}=\frac{1}{\bar{\nu}_{(n=3)}}=\frac{1}{15232.9167}=6.5647\times10^{-5}}$ cm
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 6.5647 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 656.47 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=3)}}$ = 656.47 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 620-750 nm
• We have seen that there is no clear cut boundaries between the colors in the visible spectrum
♦ There is a slow gradation from one color to another
♦ Towards '750 nm', there will be more redness
♦ Towards '620 nm', there will be more yellowness
(ii) The value we obtained using the expression given by Balmer is 656.47 nm
• It falls within the range 620-750 nm
• '656.47 nm' will have the influence of red, orange and yellow
• This is the color of the right most reddish line in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 656.47 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the emission spectrum
11. Let us put n = 4
• We get: $\mathbf\small{\bar{\nu}_{(n=4)}=109677\left(\frac{1}{2^2}-\frac{1}{4^2}\right)}$ = 20564.4375 cm-1
⇒ $\mathbf\small{\lambda_{(n=4)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{20564.4375}=4.8628\times10^{-5}}$ cm
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 4.8628 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 486.28 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 486.28 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 450-495 nm♦ This is the range of blue light
• Consider the wavelength range: 495-570 nm
♦ This is the range of green light
(ii) The value we obtained using the equation given by Balmer is 486.28 nm
• It falls within the range 450-495 nm
• So it must be blue light
♦ But note that, 486.28 is close to 495, which is the boundary between blue and green
♦ We know that, there is no clear cut boundary lines between the colors in the visible spectrum
♦ There is a gradual gradation from one color to another
♦ So 486.28 is mostly blue, with some influence of green
• It is clear that, 486.28 nm is the wavelength of the greenish blue line (second from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 486.28 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the second line from the right in the emission spectrum
12. Let us put n = 5
• Following the same procedure as above, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 434.17 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 450-425 nm
• This is the range of indigo light
• That is., if any radiation have a wavelength between 450 and 425 nm, it would be an indigo light
(ii) The value we obtained using the equation given by Balmer is 434.17 nm
• It falls within the range 450-425 nm
• So it is indigo light
• This is the wavelength corresponding to the indigo line (third line from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 434.17 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the third line from the right in the emission spectrum
13. Let us put n = 6
• We get: $\mathbf\small{\lambda_{(n=6)}}$ = 410.29 nm
• So, using the expression given by Balmer, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.23?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 425-380 nm
• This is the range of violet light
(ii) The value we obtained using the equation given by Balmer is 410.29 nm
• It falls within the range 425-380 nm
• So it is violet light
• This is the wavelength corresponding to the violet line (fourth line from the right) in fig.2.23
(iii) Let us elaborate:
• When electricity was passed through the hydrogen gas, an electron absorbed a radiation having wavelength 410.29 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the fourth line from the right in the emission spectrum
14. Since the wavelength corresponding to each line is known, we can plot them on our familiar graph. This is shown in fig.2.24 below:
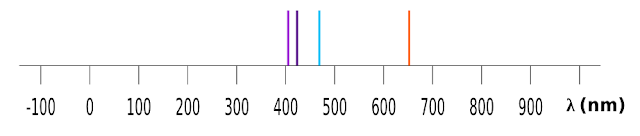 |
| Fig.2.24 |
• 380-750 nm is the range of visible light
■ So we can write:
All lines given by Balmer's expression, fall within the visible range of the electromagnetic spectrum
• Now we know the significance of the expression given by Balmer. But the following points should be noted
(i) A reddish line occurs at the point 656.47 on the graph
(ii) A greenish blue line occurs at the point 486.28 on the graph
(iii) An indigo line occurs at the point 434.17 on the graph
(iv) A violet line occurs at the point 410.29 on the graph
2. After analyzing the above data, Balmer discovered the mathematical relation between the points
• This relation is the expression that we saw in (9) above
• So Balmer gave a 'mathematical relation'. He did not say any thing about the 'structure of the atom'
• We too can derive the same expression if we have a sound knowledge in advanced mathematics. All we would need is the data in (1). We would not need to know the 'structure of atom'
3. However, Balmer's expression helped Niels Bohr very much in his research works
• Also, the lines in fig.2.23 are considered together as a set, and is given the name: Balmer Series
• So the hydrogen atoms emitted some radiations
■ Do the hydrogen atoms emit invisible radiations?
• They certainly do
• Hard copy of such radiations can be obtained in special photographic plates
• We must analyze those invisible radiations too
The Lyman series
1. Like the Balmer series, there is another ‘series of lines’ to the left of the violet color
• This series is called the Lyman series
• It was discovered by Theodore Lyman
2. Since they have wavelengths less than violet, the radiations corresponding to those lines will be invisible
• The hard copy obtained in special photographic plate is shown in fig.2.25 below:
 |
| Fig.2.25 |
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{1^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 2 (ie., n = 2, 3, 4, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 12
(ii) The least possible value of ‘n’ has changed from 3 to 2
5. Let us first put n = 2
• We get: $\mathbf\small{\bar{\nu}_{(n=2)}=109677\left(\frac{1}{1^2}-\frac{1}{2^2}\right)}$ = 82257.75 cm-1
⇒ $\mathbf\small{\lambda_{(n=2)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{82257.75}}$ = 1.2157 × 10-5 cm
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 1.2157 × 10-7 m
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 121.57 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=2)}}$ = 121.57 nm
• So, using the expression for Lyman series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.25?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 10-400 nm
This is the range corresponding to ultraviolet radiations
(ii) The value we obtained using the expression for Lyman series is 121.57 nm
• It falls within the range 10-400 nm
• So 121.57 nm is the wavelength corresponding to the right most line in Lyman series in fig.2.24
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 121.57 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Lyman series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Lyman series
For n = 3, we get: $\mathbf\small{\lambda_{(n=3)}}$ = 102.57 nm
♦ The second line from the right in the Lyman series corresponds to this wavelength
For n = 4, we get: $\mathbf\small{\lambda_{(n=4)}}$ = 97.26 nm
♦ The third line from the right in the Lyman series corresponds to this wavelength
For n = 5, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 94.98 nm
♦ The fourth line from the right in the Lyman series corresponds to this wavelength
All these wavelengths fall within the range 10-400 nm
7. So we can write:
The Lyman series falls in the ultra violet region of the electromagnetic spectrum
The Paschen series
1. Like the Balmer series and Lyman series, there is another ‘series of lines’• This series falls to the right of the red color
• This series is called the Paschen series
• It was discovered by Friedrich Paschen
2. Since they have wavelengths greater than red, the radiations corresponding to those lines will be invisible
The hard copy obtained in special photographic plate is shown in fig.2.26 below:
 |
| Fig.2.26 |
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{3^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 3 (ie., n = 4, 5, 6, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 32
(ii) The least possible value of ‘n’ has changed from 3 to 4
5. Let us first put n = 4
• We get: $\mathbf\small{\bar{\nu}_{(n=4)}=109677\left(\frac{1}{3^2}-\frac{1}{4^2}\right)}$ = 5331.520 cm-1
⇒ $\mathbf\small{\lambda_{(n=4)}=\frac{1}{\bar{\nu}_{(n=4)}}=\frac{1}{5331.520}}$ = 1.87564 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1.87564 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1875.64 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=4)}}$ = 1875.64 nm
• So, using the expression for Paschen series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum in fig.2.26?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Paschen series is 1875.64 nm
• It falls within the range 750 nm - 106 nm
• So 1875.64 nm is the wavelength corresponding to the right most line in Paschen series in fig.2.25
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 1875.64 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Paschen series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Paschen series
For n = 5, we get: $\mathbf\small{\lambda_{(n=5)}}$ = 1282.17 nm
♦ The second line from the right in the Paschen series corresponds to this wavelength
For n = 6, we get: $\mathbf\small{\lambda_{(n=6)}}$ = 1094.12 nm
♦ The third line from the right in the Paschen series corresponds to this wavelength
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 1005.22 nm
♦ The fourth line from the right in the Paschen series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Paschen series falls in the infrared region of the electromagnetic spectrum
The Brackett series
1. There is another ‘series of lines’ to the right of the Paschen series• This series is called the Brackett series
• It was discovered by Frederick Sumner Brackett
2. These lines also correspond to invisible radiations
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{4^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 5 (ie., n = 5, 6, 7, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 42
(ii) The least possible value of ‘n’ has changed from 3 to 5
5. Let us first put n = 5
• We get: $\mathbf\small{\bar{\nu}_{(n=5)}=109677\left(\frac{1}{4^2}-\frac{1}{5^2}\right)}$ = 2467.7325 cm-1
⇒ $\mathbf\small{\lambda_{(n=5)}=\frac{1}{\bar{\nu}_{(n=5)}}=\frac{1}{2467.7325}}$ = 4.0523 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4.0523 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4052.3 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=5)}}$ = 4052.3 nm
• So, using the expression for Brackett series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Paschen series is 4052.3 nm
• It falls within the range 750 nm - 106 nm
• So 4052.3 nm is the wavelength corresponding to the right most line in Brackett series
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 4052.3 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Brackett series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Brackett series
For n = 6, we get: $\mathbf\small{\lambda_{(n=6)}}$ = 2625.89 nm
♦ The second line from the right in the Brackett series corresponds to this wavelength
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 2166.14 nm
♦ The third line from the right in the Brackett series corresponds to this wavelength
For n = 8, we get: $\mathbf\small{\lambda_{(n=8)}}$ = 1945.11 nm
♦ The fourth line from the right in the Brackett series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Brackett series falls in the infrared region of the electromagnetic spectrum
The Pfund series
1. There is another ‘series of lines’ to the right of the Brackett series• This series is called the Pfund series
• It was discovered by August Herman Pfund
2. These lines also correspond to invisible radiations
3. The wave number and hence the wavelengths of the radiations corresponding to those lines can be calculated using the expression:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{5^2}-\frac{1}{n^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n is an integer equal to or greater than 6 (ie., n = 6, 7, 8, . . .)
♦ Note that, ‘n’ has to be an integer. It cannot be a fraction or decimal
4. This expression is very similar to the expression given by Balmer
• The only differences are these:
(i) The denominator of the first fraction has changed from 22 to 52
(ii) The least possible value of ‘n’ has changed from 3 to 6
5. Let us first put n = 6
• We get: $\mathbf\small{\bar{\nu}_{(n=6)}=109677\left(\frac{1}{5^2}-\frac{1}{6^2}\right)}$ = 1340.49667 cm-1
⇒ $\mathbf\small{\lambda_{(n=6)}=\frac{1}{\bar{\nu}_{(n=6)}}=\frac{1}{1340.49667}}$ = 7.45992 × 10-4 cm
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7.45992 × 10-6 m
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7459.92 × 10-9 m
⇒ $\mathbf\small{\lambda_{(n=6)}}$ = 7459.92 nm
• So, using the expression for Pfund series, we calculated a wavelength. Is there any relation between this wavelength and the emission spectrum?
Answer can be written in 3 steps:
(i) Consider the wavelength range: 750 nm - 106 nm
This is the range corresponding to infrared radiations
(ii) The value we obtained using the expression for Pfund series is 7459.92 nm
• It falls within the range 750 nm - 106 nm
• So 4052.3 nm is the wavelength corresponding to the right most line in Pfund series
(iii) Let us elaborate:
• An electron in the hydrogen gas, absorbed a radiation having wavelength 7459.92 nm
• Naturally, that electron would be promoted to a higher energy level
• When it returned to the ground state, it emitted the same radiation
• This 'emitted radiation' appeared as the right most line in the Pfund series in the emission spectrum
6. In a similar way, we can find the wavelengths corresponding to the other lines in the Pfund series
For n = 7, we get: $\mathbf\small{\lambda_{(n=7)}}$ = 4653.82 nm
♦ The second line from the right in the Pfund series corresponds to this wavelength
For n = 8, we get: $\mathbf\small{\lambda_{(n=8)}}$ = 3740.59 nm
♦ The third line from the right in the Pfund series corresponds to this wavelength
For n = 9, we get: $\mathbf\small{\lambda_{(n=9)}}$ = 3297.02 nm
♦ The fourth line from the right in the Pfund series corresponds to this wavelength
All these wavelengths fall within the range 750 nm - 106 nm
7. So we can write:
The Pfund series falls in the infrared region of the electromagnetic spectrum
• We have seen the various ‘series of lines’ in the emission spectrum of hydrogen
• We see that, there is a regular pattern
• Because of the regular pattern, a ‘general expression’ can be derived
• This ‘general expression’ will represent all the expressions. It is given below:
$\mathbf\small{\bar{\nu}=109677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)}$
• Where:
♦ $\mathbf\small{\bar{\nu}}$ is the wave number
♦ n1 is an integer equal to or greater than 1 (ie., n1 = 1, 2, 3, . . .)
♦ n2 is equal to [(n1+1), (n1+2), (n1+3), . . . ]
♦ Note that, ‘n1’ has to be an integer. It cannot be a fraction or decimal
♦ When ‘n1’ is an integer, n2 will naturally become an integer
■ In the general expression,
♦ when we put n1 = 1, we get the Lyman series
♦ when we put n1 = 2, we get the Balmer series
♦ when we put n1 = 3, we get the Paschen series
♦ so on . . .
■ This general expression was derived by Swedish spectroscopist Johannes Rydberg
• He derived this expression independently. That is., he did not have any knowledge about the discoveries made by Lyman, Balmer, Paschen, Brackett and Pfund
■ So we can write:
• Lyman, Balmer, Paschen, Brackett and Pfund discovered the various series
• Rydberg independently discovered the expression which can represent any series in the hydrogen spectrum
• The value '109677 cm-1' is named as Rydberg constant for Hydrogen in his honor
■ Let us find the unit of '109677':
♦ In the general expression, we have $\mathbf\small{\bar{\nu}}$ on the left side
♦ The unit of $\mathbf\small{\bar{\nu}}$ is cm-1
♦ On the right side, the 'quantities within brackets' are numbers. They do not have any units
♦ So the unit of '109677' is cm-1.
• As mentioned in the case of Balmer's expression, this general expression is also based on mathematical calculations
• It does not tell us any thing about the 'structure of hydrogen atom'
• It was Neils Bohr who cracked the mystery
• The regular patterns seen in the various series, helped Bohr in his research. We will learn about his works in the next section
• It does not tell us any thing about the 'structure of hydrogen atom'
• It was Neils Bohr who cracked the mystery
• The regular patterns seen in the various series, helped Bohr in his research. We will learn about his works in the next section
No comments:
Post a Comment