In the previous section, we saw the drawbacks of Rutherford model of atom. The Rutherford model was further improved by the Danish scientist Neils Bohr
• The studies made by Neils Bohr were based on the following two items:
(i) Dual nature of electromagnetic radiations
♦ Electromagnetic radiations possess wave like properties
♦ Electromagnetic radiations possess particle like properties also
(ii) Results obtained from experiments on atomic spectra
• So to learn about the Bohr model, we must first learn about the basic properties of electromagnetic radiations (item i)
• Also we have to learn about atomic spectra (item ii)
• In this section and the following section, we will discuss about those two topics
• The up and down oscillation is indicated by the white double headed arrow
2. An electrically charged particle will have an electric field around it
• Our particle is oscillating. So the electric field changes
• The changing electric field is indicated by the cyan wave in fig.2.8
• We see that:
♦ Alternate portions of the cyan wave are in the +ve z region
♦ Alternate portions of the cyan wave are in the -ve z region
♦ This gives the indication that, the 'electric field is changing'
3. A 'changing electric field' will give rise to a magnetic field
• So in our present case, a magnetic field will also be produced
• This magnetic field will also be of changing nature
• It is indicated by the yellow wave in fig.2.8
• We see that:
♦ Alternate portions of the yellow wave are in the +ve y region
♦ Alternate portions of the yellow wave are in the -ve y region
♦ This gives the indication that, the magnetic field is changing
4. A changing magnetic field will in turn give rise to a changing electric field
• So a cyclic process will be set up as shown below:
• Due to this cyclic process, a wave begins to be emitted from the charged particle
5. We see that, the wave emitted by the charged particle has two fields:
• An electric field and a magnetic field
■ Such a wave is called an electromagnetic wave
6. The planes in which the two waves lie, are shown in the fig.2.9 below
• The cyan electric wave lies in a cyan plane
♦ This cyan plane is in fact the xz-plane
• The yellow magnetic wave lies in a yellow plane
♦ This yellow plane is in fact the xy-plane
7. We know that, in the Cartesian coordinate system, the xy-plane is perpendicular to the xz-plane
• So we can say that, the electric field and magnetic field are perpendicular to each other
8. The electric wave lies in the xz-plane
♦ It oscillates up and down in the xz-plane
♦ We see that, the up and down oscillation is in the z direction
■ So the oscillation of the electric wave is in the z direction
9. The magnetic wave lies in the xy-plane
♦ It oscillates to and fro in the xy-plane
♦ We see that, the to and fro oscillation is in the y direction
■ So the oscillation of the magnetic wave is in the y direction
10. Also in the fig., the propagation of the wave is in the x direction
11. So the following three quantities are perpendicular to each other:
(i) Direction of oscillation of the magnetic wave
(ii) Direction of oscillation of the electric wave
(iii) Direction of propagation of the wave
12. Next we will see some properties of electromagnetic waves
• In our previous classes, we have learned some basic properties of ordinary waves (Details here)
• We saw frequency ($\mathbf\small{\nu}$), wavelength ($\mathbf\small{\lambda}$) and amplitude (A)
• We saw some calculations also, related to those waves
♦ Like finding the velocity, time period etc.,
13. The waves that we saw in those previous classes were simple waves
• They did not have different components like electric component, magnetic component etc.,
• But there is nothing to worry about
• We can apply those same calculations here also
14. Why are we able to apply the same calculations ?
• The reason can be explained in five steps:
(i) Both the electric and magnetic components have the same frequency
(ii) Both the electric and magnetic components have the same wavelength
(iii) Both the electric and magnetic components have the same amplitude
(iv) Both the electric and magnetic components are in phase
(v) ‘In phase’ means that:
• When one field becomes zero, the other field also becomes zero
• When one field attains the maximum value (amplitude), the other field also attains the maximum value
• This is obvious because, both the waves intersect at the same points on the x axis
15. We know that sound waves require a medium to travel
• But the electromagnetic waves do not require a medium. They can travel even in vacuum
16. The frequency of an electromagnetic wave is denoted by the symbol ($\mathbf\small{\lambda}$)
♦ The unit is Hz
♦ This 'Hz' is same as 's-1'
17. The wavelength of an electromagnetic wave is denoted by the symbol ($\mathbf\small{\nu}$)
♦ The unit is m
18. We know that, velocity of a wave (v) is given by: Velocity = Frequency × Wavelength
• This is true for electromagnetic waves also
• In vacuum all electromagnetic waves travel at the same speed of 3 × 108 ms-1
• This is called the speed of light. It’s symbol is c
■ So for electromagnetic waves, we get: $\mathbf\small{c=\nu \lambda}$
19. The speed of light is a constant
■ So it is clear that, when frequency increases, wavelength decreases and vice versa
• Next we will see the various electromagnetic waves that occur (naturally or artificially) around us
1. We know that white light is composed of seven different lights:
Violet, indigo, blue, green, yellow, orange and red
(Details here)
2. Each of these lights is an electromagnetic wave
Let us elaborate:
• Violet light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 425 – 400 nm
♦ The frequency of this electromagnetic wave lies between 700 × 1012 - 750 × 1012 Hz
• Indigo light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 450 - 425 nm
♦ The frequency of this electromagnetic wave lies between 670 × 1012 - 700 × 1012 Hz
• Blue light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 500 - 450 nm
♦ The frequency of this electromagnetic wave lies between 600 × 1012 – 670 × 1012 Hz
_ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _
• Red light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 750 - 610 nm
♦ The frequency of this electromagnetic wave lies between 480 × 1012 - 400 × 1012 Hz
3. We can plot the above wavelengths on a graph
• In fig.2.10 below, the bottom line is divided into equal parts
♦ We see that, each division is equal to 100 nm
♦ So, for this graph, the scale is: 1 unit = 100 nm
4. As we go towards the right, the wavelength increases
• The violet light has a lowest wavelength of 400 nm. So it is plotted from 400 nm towards the right
• The red light has a highest wavelength of 750 nm. So it is plotted from 750 nm towards the left
• All other lights come in between violet and red
5. As science progressed, more and more electromagnetic waves came to be known to us. Let us see two of them
(i) The ultra violet waves
• The wavelength lies between 380 – 10 nm
♦ The highest value is 380
♦ This '380' is less than the lowest value (400) of violet
♦ So ultraviolet comes to the left of violet
♦ It is shown in fig.2.11 below:
• The frequency lies between 8 × 1014 to 300 × 1014 Hz
♦ The lowest value is 8 × 1014
♦ This '8 × 1014' is higher than the highest value (750 × 1012) of violet
(ii) The infrared waves
• The wavelength lies between 750 nm – 106 nm
♦ The lowest value is 750
♦ This '750' is same as the highest value (750) of red
♦ So infrared comes to the right of red
♦ It is shown in fig.2.11 above
♦ The upper boundary of '106' is so large that, it does not fit into the fig.
♦ So a double arrow is shown
• The frequency lies between 430000 × 109 to 300 × 109 Hz
♦ The highest value is 430000 × 109
♦ This '430000 × 109' is lower than the lowest value (400 × 1012) of red
6. If the wavelength of an electromagnetic wave is less than 400 nm (lowest wavelength of violet), it will not be visible to our naked eyes
♦ Special instruments are required to detect such invisible waves
• Also, if the wavelength of an electromagnetic wave is greater than 750 nm (highest wavelength of red), it will not be visible to our naked eyes
♦ Special instruments are required to detect such invisible waves also
■ The wavelength range from violet (400 nm) to red (750 nm) is called the visible spectrum
7. There are even more electromagnetic waves:
• X-rays which fall to the left of ultraviolet rays
♦ X-rays fall to the left of ultraviolet rays because, the former has lesser wavelengths
• 𝛾-rays which fall to the left of X-rays
♦ 𝛾-rays fall to the left of X-rays because, the former has lesser wavelengths
• Microwaves which fall to the right of infrared waves
♦ Microwaves fall to the right of infrared waves because, the former has greater wavelengths
• Radio waves which fall to the right of micro waves
♦ Radio waves fall to the right of micro waves because, the former has greater wavelengths
• Long radio waves which fall to the right of radio waves
♦ Long radio waves fall to the right of radio waves because, the former has greater wavelengths
8. So we have the 𝛾-rays at the left end and Long radio waves at the right end
• For the graph in fig.7.10 and 7.11, we used the scale: 1 unit = 100 nm
• Even if we use a larger scale like 1 unit = 10000 nm, it is not possible to draw the graph of all the waves (from 𝛾-rays to long radio waves) on an ordinary sheet of paper
9. So we use a logarithmic scale
• Such a graph is shown in fig.2.12 below
• It is obtained from wikimedia commons. The link is given below:
https://commons.wikimedia.org/wiki/File:EM_spectrum.svg
10. In fig.7.12, we see that, the markings on the x axis are all powers of 10
• Consider any two adjacent marks, say 10-12 and 10-10
♦ We have: 10-12 × 100 = 10-10
• In this way, all marks are obtained by multiplying the preceding marks (on the left) by 100
• In ordinary scales, each mark is obtained by adding a 'particular value' to the preceding mark
• In logarithmic scale, each mark is obtained by multiplying the preceding mark by a 'particular power of 10'
11. This type of scale is useful when the values to be plotted fall in a very wide range
• In our present case, the range is: 10-16 to 108
12. We will learn the details about logarithmic scales in math classes
■ The important point to note for our present case is this:
If wave length increases towards the right, frequency decreases towards the right
• This is because, wavelength ($\mathbf\small{\lambda}$) is inversely proportional to frequency ($\mathbf\small{\nu}$)
• This is evident from the relation: $\mathbf\small{c=\nu \lambda}$
■The different electromagnetic radiations shown in fig.7.12 constitute what is called the electromagnetic spectrum
Solved example 2.17
The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of 1,368 kHz (kilo hertz). Calculate the wavelength of the electromagnetic radiation emitted by transmitter. Which part of the electromagnetic spectrum does it belong to?
Solution:
1. Given that $\mathbf\small{\nu}$ = 1368 × 103 Hz
2. We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\lambda=\frac{c}{\nu}}$
3. Substituting the values, we get: $\mathbf\small{\lambda=\frac{3\times 10^8 \rm{(ms^{-1})}}{1368\times 10^3\rm{(s^{-1})}}}$ = 219.3 m
4. The wavelength of Radio waves fall in the range: 1 mm to 10000 km
• '219.3 m' lies within this range
Solved example 2.18
The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz). (1 nm = 10-9 m)
Solution:
1. Violet:
• Given that $\mathbf\small{\lambda}$ = 400 × 10-9 m
• We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{400\times 10^{-9}\rm{(m)}}}$ = 7.50 × 1014 s-1 = 7.50 × 1014 Hz
2. Red:
• Given that $\mathbf\small{\lambda}$ = 750 × 10-9 m
• We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{750\times 10^{-9}\rm{(m)}}}$ = 4.00 × 1014 s-1 = 4.00 × 1014 Hz
Solved example 2.19
Calculate (a) wavenumber and (b) frequency of yellow radiation having wavelength 5800 $\mathbf\small{\mathring{A}}$
Solution:
■ Wavenumber is defined as the number of wavelengths in unit length
• The SI unit of length is m
• So we can write:
Wavenumber is the number of wavelengths in one m
• It's symbol is $\mathbf\small{\bar{\nu}}$
• Thus we get: $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}}$
Part (a):
• Given that $\mathbf\small{\lambda=5800\;\mathring{A}}$ = 5800 × 10-10 m
• So $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}=\frac{1}{5800\times10^{-10}\;\rm{(m)}}}$ = 1.724 × 106 m-1
Part (b):
• We have: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{5800\times 10^{-10}\rm{(m)}}}$ = 5.172 × 1014 s-1 = 4.00 × 1014 Hz
Solved example 2.20
Calculate the wavelength, frequency and wavenumber of a light wave whose period is 2.0 × 10-10 s.
Solution:
1. We have frequency ($\mathbf\small{\nu}$) = $\mathbf\small{\frac{1}{T}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{1}{2\times 10^{-10}\; \rm{(s)}}}$ = 5 × 109 s-1
2. We have: $\mathbf\small{\lambda=\frac{c}{\nu}}$
• Substituting the values, we get:
$\mathbf\small{\lambda=\frac{3\times 10^8 \rm{(ms^{-1})}}{5\times 10^9\rm{(s^{-1})}}}$ = 0.06 m
3. We have: $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}}$
• Substituting the values, we get:
$\mathbf\small{\bar{\nu}=\frac{1}{0.06\;\rm{(m)}}}$ = 16.66 m-1
Solved example 2.21
Write a method for making a connection between the $\mathbf\small{\lambda}$ axis and the $\mathbf\small{\nu}$ axis in the electromagnetic spectrum
Solution:
1. Consider the relation $\mathbf\small{\nu=\frac{c}{\lambda}}$
• 'c' in the numerator has the value 3 × 108 ms-1
• So if we put '300 × 10-9 m' (a wavelength in the ultra violet region) in the denominator, the two '3' s will cancel each other. Then corresponding $\mathbf\small{\nu}$ will have 'powers of 10' only
2. We can write:
$\mathbf\small{\nu}$ corresponding to a wavelength of 300 × 10-9 m
= $\mathbf\small{\frac{3\times 10^8 \rm{(ms^{-1})}}{300\times 10^{-9}\rm{(m)}}}$
= 1015 s-1
3. Now we can apply this result:
(i) On the $\mathbf\small{\lambda}$ axis, mark point P corresponding to 300 × 10-9 m
(ii) Draw a vertical red dashed line through P
This is shown in fig.2.13 below:
(iii) Mark the point of intersection of the red dashed line and the $\mathbf\small{\nu}$ axis as Q
(iv) Then Q corresponds to 1015 Hz
(v) Once '1015' is fixed, we can mark other points 1012 , 1014, 1016, 1018 etc., on the $\mathbf\small{\nu}$ axis
• The studies made by Neils Bohr were based on the following two items:
(i) Dual nature of electromagnetic radiations
♦ Electromagnetic radiations possess wave like properties
♦ Electromagnetic radiations possess particle like properties also
(ii) Results obtained from experiments on atomic spectra
• So to learn about the Bohr model, we must first learn about the basic properties of electromagnetic radiations (item i)
• Also we have to learn about atomic spectra (item ii)
• In this section and the following section, we will discuss about those two topics
Wave nature of electromagnetic radiations
1. In the fig.2.8 below, an electrically charged particle (shown as a red sphere) is oscillating up and down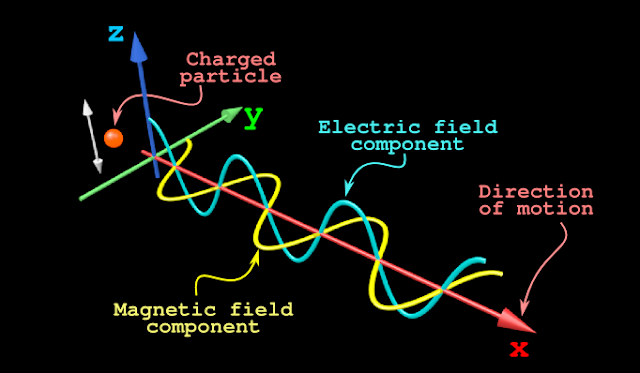 |
| Fig.2.8 |
2. An electrically charged particle will have an electric field around it
• Our particle is oscillating. So the electric field changes
• The changing electric field is indicated by the cyan wave in fig.2.8
• We see that:
♦ Alternate portions of the cyan wave are in the +ve z region
♦ Alternate portions of the cyan wave are in the -ve z region
♦ This gives the indication that, the 'electric field is changing'
3. A 'changing electric field' will give rise to a magnetic field
• So in our present case, a magnetic field will also be produced
• This magnetic field will also be of changing nature
• It is indicated by the yellow wave in fig.2.8
• We see that:
♦ Alternate portions of the yellow wave are in the +ve y region
♦ Alternate portions of the yellow wave are in the -ve y region
♦ This gives the indication that, the magnetic field is changing
4. A changing magnetic field will in turn give rise to a changing electric field
• So a cyclic process will be set up as shown below:
• Due to this cyclic process, a wave begins to be emitted from the charged particle
5. We see that, the wave emitted by the charged particle has two fields:
• An electric field and a magnetic field
■ Such a wave is called an electromagnetic wave
6. The planes in which the two waves lie, are shown in the fig.2.9 below
 |
| Fig.2.9 |
♦ This cyan plane is in fact the xz-plane
• The yellow magnetic wave lies in a yellow plane
♦ This yellow plane is in fact the xy-plane
7. We know that, in the Cartesian coordinate system, the xy-plane is perpendicular to the xz-plane
• So we can say that, the electric field and magnetic field are perpendicular to each other
8. The electric wave lies in the xz-plane
♦ It oscillates up and down in the xz-plane
♦ We see that, the up and down oscillation is in the z direction
■ So the oscillation of the electric wave is in the z direction
9. The magnetic wave lies in the xy-plane
♦ It oscillates to and fro in the xy-plane
♦ We see that, the to and fro oscillation is in the y direction
■ So the oscillation of the magnetic wave is in the y direction
10. Also in the fig., the propagation of the wave is in the x direction
11. So the following three quantities are perpendicular to each other:
(i) Direction of oscillation of the magnetic wave
(ii) Direction of oscillation of the electric wave
(iii) Direction of propagation of the wave
12. Next we will see some properties of electromagnetic waves
• In our previous classes, we have learned some basic properties of ordinary waves (Details here)
• We saw frequency ($\mathbf\small{\nu}$), wavelength ($\mathbf\small{\lambda}$) and amplitude (A)
• We saw some calculations also, related to those waves
♦ Like finding the velocity, time period etc.,
13. The waves that we saw in those previous classes were simple waves
• They did not have different components like electric component, magnetic component etc.,
• But there is nothing to worry about
• We can apply those same calculations here also
14. Why are we able to apply the same calculations ?
• The reason can be explained in five steps:
(i) Both the electric and magnetic components have the same frequency
(ii) Both the electric and magnetic components have the same wavelength
(iii) Both the electric and magnetic components have the same amplitude
(iv) Both the electric and magnetic components are in phase
(v) ‘In phase’ means that:
• When one field becomes zero, the other field also becomes zero
• When one field attains the maximum value (amplitude), the other field also attains the maximum value
• This is obvious because, both the waves intersect at the same points on the x axis
15. We know that sound waves require a medium to travel
• But the electromagnetic waves do not require a medium. They can travel even in vacuum
16. The frequency of an electromagnetic wave is denoted by the symbol ($\mathbf\small{\lambda}$)
♦ The unit is Hz
♦ This 'Hz' is same as 's-1'
17. The wavelength of an electromagnetic wave is denoted by the symbol ($\mathbf\small{\nu}$)
♦ The unit is m
18. We know that, velocity of a wave (v) is given by: Velocity = Frequency × Wavelength
• This is true for electromagnetic waves also
• In vacuum all electromagnetic waves travel at the same speed of 3 × 108 ms-1
• This is called the speed of light. It’s symbol is c
■ So for electromagnetic waves, we get: $\mathbf\small{c=\nu \lambda}$
19. The speed of light is a constant
■ So it is clear that, when frequency increases, wavelength decreases and vice versa
• We have seen the basic properties of electromagnetic waves
1. We know that white light is composed of seven different lights:
Violet, indigo, blue, green, yellow, orange and red
(Details here)
2. Each of these lights is an electromagnetic wave
Let us elaborate:
• Violet light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 425 – 400 nm
♦ The frequency of this electromagnetic wave lies between 700 × 1012 - 750 × 1012 Hz
• Indigo light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 450 - 425 nm
♦ The frequency of this electromagnetic wave lies between 670 × 1012 - 700 × 1012 Hz
• Blue light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 500 - 450 nm
♦ The frequency of this electromagnetic wave lies between 600 × 1012 – 670 × 1012 Hz
_ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _
• Red light is an electromagnetic wave
♦ It has an electric field and a magnetic field
♦ The wavelength of this electromagnetic wave lies between 750 - 610 nm
♦ The frequency of this electromagnetic wave lies between 480 × 1012 - 400 × 1012 Hz
3. We can plot the above wavelengths on a graph
• In fig.2.10 below, the bottom line is divided into equal parts
♦ We see that, each division is equal to 100 nm
♦ So, for this graph, the scale is: 1 unit = 100 nm
 |
| Fig.2.10 |
• The violet light has a lowest wavelength of 400 nm. So it is plotted from 400 nm towards the right
• The red light has a highest wavelength of 750 nm. So it is plotted from 750 nm towards the left
• All other lights come in between violet and red
5. As science progressed, more and more electromagnetic waves came to be known to us. Let us see two of them
(i) The ultra violet waves
• The wavelength lies between 380 – 10 nm
♦ The highest value is 380
♦ This '380' is less than the lowest value (400) of violet
♦ So ultraviolet comes to the left of violet
♦ It is shown in fig.2.11 below:
 |
| Fig.2.11 |
♦ The lowest value is 8 × 1014
♦ This '8 × 1014' is higher than the highest value (750 × 1012) of violet
(ii) The infrared waves
• The wavelength lies between 750 nm – 106 nm
♦ The lowest value is 750
♦ This '750' is same as the highest value (750) of red
♦ So infrared comes to the right of red
♦ It is shown in fig.2.11 above
♦ The upper boundary of '106' is so large that, it does not fit into the fig.
♦ So a double arrow is shown
• The frequency lies between 430000 × 109 to 300 × 109 Hz
♦ The highest value is 430000 × 109
♦ This '430000 × 109' is lower than the lowest value (400 × 1012) of red
6. If the wavelength of an electromagnetic wave is less than 400 nm (lowest wavelength of violet), it will not be visible to our naked eyes
♦ Special instruments are required to detect such invisible waves
• Also, if the wavelength of an electromagnetic wave is greater than 750 nm (highest wavelength of red), it will not be visible to our naked eyes
♦ Special instruments are required to detect such invisible waves also
■ The wavelength range from violet (400 nm) to red (750 nm) is called the visible spectrum
7. There are even more electromagnetic waves:
• X-rays which fall to the left of ultraviolet rays
♦ X-rays fall to the left of ultraviolet rays because, the former has lesser wavelengths
• 𝛾-rays which fall to the left of X-rays
♦ 𝛾-rays fall to the left of X-rays because, the former has lesser wavelengths
• Microwaves which fall to the right of infrared waves
♦ Microwaves fall to the right of infrared waves because, the former has greater wavelengths
• Radio waves which fall to the right of micro waves
♦ Radio waves fall to the right of micro waves because, the former has greater wavelengths
• Long radio waves which fall to the right of radio waves
♦ Long radio waves fall to the right of radio waves because, the former has greater wavelengths
8. So we have the 𝛾-rays at the left end and Long radio waves at the right end
• For the graph in fig.7.10 and 7.11, we used the scale: 1 unit = 100 nm
• Even if we use a larger scale like 1 unit = 10000 nm, it is not possible to draw the graph of all the waves (from 𝛾-rays to long radio waves) on an ordinary sheet of paper
9. So we use a logarithmic scale
• Such a graph is shown in fig.2.12 below
• It is obtained from wikimedia commons. The link is given below:
https://commons.wikimedia.org/wiki/File:EM_spectrum.svg
 |
| Fig.2.12 |
• Consider any two adjacent marks, say 10-12 and 10-10
♦ We have: 10-12 × 100 = 10-10
• In this way, all marks are obtained by multiplying the preceding marks (on the left) by 100
• In ordinary scales, each mark is obtained by adding a 'particular value' to the preceding mark
• In logarithmic scale, each mark is obtained by multiplying the preceding mark by a 'particular power of 10'
11. This type of scale is useful when the values to be plotted fall in a very wide range
• In our present case, the range is: 10-16 to 108
12. We will learn the details about logarithmic scales in math classes
■ The important point to note for our present case is this:
If wave length increases towards the right, frequency decreases towards the right
• This is because, wavelength ($\mathbf\small{\lambda}$) is inversely proportional to frequency ($\mathbf\small{\nu}$)
• This is evident from the relation: $\mathbf\small{c=\nu \lambda}$
■The different electromagnetic radiations shown in fig.7.12 constitute what is called the electromagnetic spectrum
Now we will see some solved examples
The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of 1,368 kHz (kilo hertz). Calculate the wavelength of the electromagnetic radiation emitted by transmitter. Which part of the electromagnetic spectrum does it belong to?
Solution:
1. Given that $\mathbf\small{\nu}$ = 1368 × 103 Hz
2. We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\lambda=\frac{c}{\nu}}$
3. Substituting the values, we get: $\mathbf\small{\lambda=\frac{3\times 10^8 \rm{(ms^{-1})}}{1368\times 10^3\rm{(s^{-1})}}}$ = 219.3 m
4. The wavelength of Radio waves fall in the range: 1 mm to 10000 km
• '219.3 m' lies within this range
Solved example 2.18
The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz). (1 nm = 10-9 m)
Solution:
1. Violet:
• Given that $\mathbf\small{\lambda}$ = 400 × 10-9 m
• We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{400\times 10^{-9}\rm{(m)}}}$ = 7.50 × 1014 s-1 = 7.50 × 1014 Hz
2. Red:
• Given that $\mathbf\small{\lambda}$ = 750 × 10-9 m
• We have: $\mathbf\small{c=\nu \lambda}$
From this we get: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{750\times 10^{-9}\rm{(m)}}}$ = 4.00 × 1014 s-1 = 4.00 × 1014 Hz
Solved example 2.19
Calculate (a) wavenumber and (b) frequency of yellow radiation having wavelength 5800 $\mathbf\small{\mathring{A}}$
Solution:
■ Wavenumber is defined as the number of wavelengths in unit length
• The SI unit of length is m
• So we can write:
Wavenumber is the number of wavelengths in one m
• It's symbol is $\mathbf\small{\bar{\nu}}$
• Thus we get: $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}}$
Part (a):
• Given that $\mathbf\small{\lambda=5800\;\mathring{A}}$ = 5800 × 10-10 m
• So $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}=\frac{1}{5800\times10^{-10}\;\rm{(m)}}}$ = 1.724 × 106 m-1
Part (b):
• We have: $\mathbf\small{\nu=\frac{c}{\lambda}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{3\times 10^8 \rm{(ms^{-1})}}{5800\times 10^{-10}\rm{(m)}}}$ = 5.172 × 1014 s-1 = 4.00 × 1014 Hz
Solved example 2.20
Calculate the wavelength, frequency and wavenumber of a light wave whose period is 2.0 × 10-10 s.
Solution:
1. We have frequency ($\mathbf\small{\nu}$) = $\mathbf\small{\frac{1}{T}}$
• Substituting the values, we get: $\mathbf\small{\nu=\frac{1}{2\times 10^{-10}\; \rm{(s)}}}$ = 5 × 109 s-1
2. We have: $\mathbf\small{\lambda=\frac{c}{\nu}}$
• Substituting the values, we get:
$\mathbf\small{\lambda=\frac{3\times 10^8 \rm{(ms^{-1})}}{5\times 10^9\rm{(s^{-1})}}}$ = 0.06 m
3. We have: $\mathbf\small{\bar{\nu}=\frac{1}{\lambda}}$
• Substituting the values, we get:
$\mathbf\small{\bar{\nu}=\frac{1}{0.06\;\rm{(m)}}}$ = 16.66 m-1
Solved example 2.21
Write a method for making a connection between the $\mathbf\small{\lambda}$ axis and the $\mathbf\small{\nu}$ axis in the electromagnetic spectrum
Solution:
1. Consider the relation $\mathbf\small{\nu=\frac{c}{\lambda}}$
• 'c' in the numerator has the value 3 × 108 ms-1
• So if we put '300 × 10-9 m' (a wavelength in the ultra violet region) in the denominator, the two '3' s will cancel each other. Then corresponding $\mathbf\small{\nu}$ will have 'powers of 10' only
2. We can write:
$\mathbf\small{\nu}$ corresponding to a wavelength of 300 × 10-9 m
= $\mathbf\small{\frac{3\times 10^8 \rm{(ms^{-1})}}{300\times 10^{-9}\rm{(m)}}}$
= 1015 s-1
3. Now we can apply this result:
(i) On the $\mathbf\small{\lambda}$ axis, mark point P corresponding to 300 × 10-9 m
(ii) Draw a vertical red dashed line through P
This is shown in fig.2.13 below:
 |
| Fig.2.13 |
(iv) Then Q corresponds to 1015 Hz
(v) Once '1015' is fixed, we can mark other points 1012 , 1014, 1016, 1018 etc., on the $\mathbf\small{\nu}$ axis
In the next section we will see particle nature of waves

No comments:
Post a Comment