We are discussing the basics of VSEPR theory. In the previous section 4.16, we completed the discussion on 'examples which do not have lone pairs'. In this section, we will start the discussion on 'examples which do have lone pairs'
1. Let us recall the 'general forms' that we saw in the previous sections:
AB, AB2, AB3, AB4, AB5 and AB6
• These molecules do not have any lone pairs of electrons
(Note that, we are considering only 'those lone pairs which are possessed by the central atom')
2. When the molecules have lone pairs, we add 'Ei' to the general form
♦ The letter 'E' indicates the presence of lone pairs of electrons in the central atom
♦ The subscript 'i' indicates the 'number ' of lone pairs
3. Following are the 'general forms' of such molecules that we have to learn:
Case I: Number of B atoms = 2
(a) General form is: AB2E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by two B atoms
♦ A has one lone pair
(b) General form is: AB2E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by two B atoms
♦ A has two lone pairs
Case II: Number of B atoms = 3
(a) General form is: AB3E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by three B atoms
♦ A has one lone pair
(b) General form is: AB3E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by three B atoms
♦ A has two lone pairs
Case III: Number of B atoms = 4
(a) General form is: AB4E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by four B atoms
♦ A has one lone pair
(b) General form is: AB4E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by four B atoms
♦ A has two lone pairs
Case IV: Number of B atoms = 5
(a) General form is: AB5E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by five B atoms
♦ A has one lone pair
(i) The number 'i' is the 'number of lone pairs'
♦ It is not the 'number of electrons'
(ii) The 'lone pairs' are those electron pairs possessed by the central atom A
♦ The 'lone pairs' (if any), possessed by 'B atoms' are not considered in our present discussions
(i) The smallest cases mentioned above (case I with two B atoms) are AB2E and AB2E2
Why is it that, there are no smaller cases like ABE and ABE2?
(ii) The largest case mentioned above (case IV with five B atoms) is AB5E
Why is it that, there is no larger cases like AB5E2?
• We will see the answers during the course of our discussions
• We now begin the discussion with Case I (a): AB2E
We will write it in steps:
1. In AB2E, there are 2 terminal atoms and 1 electron pair
• So there is a total of 3 items
• These 3 items are distributed around A
2. Suppose that all the three items are 'sticks'
• Then there will be 3 sticks around A
• We have already seen such a case in the previous sections
• It is the molecule AB3. It has 3 sticks around A
3. When there are 3 sticks around A, the shape is trigonal planar
• This is shown in the fig.4.99(a) below:
4. But actually in our present case, we do not have 3 sticks
• We have only two sticks and one lone pair
• So from fig.4.99(a), we remove one stick
• In the place of that 'removed stick', we put a lone pair
• This is shown in fig.4.99(b)
♦ The 'removed stick' is indicated by a dashed blue line
✰ This blue dashed line help us to remember the position of the lone pair
5. Now there is a problem
• We can write the '120o' between the two bottom sticks. Because, they are two well defined sticks
• But we cannot write the '120o' on the left and right sides. The reason can be written in (iv) steps:
(i) The 'bonding electrons' are confined inside the stick
♦ This is because, they are shared by two atoms
♦ So they occupy a definite space
(ii) But 'lone electrons' are not confined. They freely occupy a region. The region is an electron cloud
(iii) We can easily measure an angle from a stick
♦ Because, a stick is well defined
(iv) But we cannot measure the angle from a cloud
♦ Because, the electron cloud does not have a well defined boundary
6. So we must remove the two '120o' angles on the left and right sides
• There is no need to specify those angles
• So the shape would be as shown in fig.4.99(c)
7. There is yet another problem:
• We had earlier obtained the 120o as follows:
The 3 sticks try to push each other as far away as possible, and they settle down with angles of '120o' between them
• But here there are no '3 sticks'. There are only '2 sticks' and a lone pair
♦ However, since they are all electrons, they will all be pushing each other
♦ But the pushing (repulsion) are different
■ We can write:
The following two repulsion are different:
(i) Repulsion between the 2 sticks
(ii) Repulsion between any one stick and a blue dashed line
So how do we finalize the angle?
8. The VSEPR theory helps us in this situation
It can be written in (iii) steps:
(i) The bond pairs are confined into sticks
(ii) But the lone pairs occupy a region
♦ As a result, the lone pairs require more space
(iii) Thus, the lone pairs are able to apply a 'greater repulsion'
• We can consider two types of repulsion: (a) and (b)
(a) Repulsion between two bond pairs
♦ This is denoted as: bond pair-bond pair repulsion (bp-bp repulsion)
♦ This is the repulsion between the two sticks
(b) Repulsion between a lone pair and a bond pair
♦ This is denoted as: lone pair-bond pair repulsion (lp-bp repulsion)
♦ This is the repulsion between the dashed blue line and a stick
■ The VSEPR theory tells us that, (b) will be greater than (a)
9. Based on this, we can think about the angle
• It can be written in (v) steps;
(i) The two sticks in fig.4.99(c), tries to maintain an angle of 120o between them
(ii) They try to maintain this angle, by using the bp-bp repulsion mentioned in (8) above
♦ This repulsion is indicated by the red double headed arrow in fig.4.100(a) below:
(iii) But the sticks are acted upon by other repulsion forces also
• The left stick is acted upon by the repulsion from the lone pair
♦ This repulsion is indicated by the left yellow double headed arrow in fig.4.100(a)
• The right stick is also acted upon by the repulsion from the lone pair
♦ This repulsion is indicated by the right yellow double headed arrow in fig.4.100(a)
(iv) From (8), we know that, the yellow arrows are stronger than the red arrow
• So the two sticks will bend further down
(v) As a result, the angle between the sticks will become less than 120o
♦ This is shown in fig.4.100(b)
♦ This fig.4.100(b) shows the final shape
10. Now we can write about the final shape. It can be written in (iii) steps
(i) The lone pair influence the shape of the atoms but they are invisible
(ii) So the final shape is determined by the positions of the atoms
(iii) We have two 'B atoms' and one 'A atom'
♦ They do not lie on a straight line. So we call it: Bent structure
• Once we finalize the shape, we no longer need to show the blue dashed line. So it is not shown in fig.4.100(b)
11. Note that, even though it is a bent structure, it is not a 3D structure. It is a 2D structure
• The reason is obvious. It can be written in steps:
(i) A plane can be made to pass through any three given points (Details here)
(ii) So there will always be a plane which contains the two B atoms and the one A atom
(iii) So this bent molecule is always planar
12. The actual value of the angle:
• In the general case, we write that: The angle will be less than 120o
♦ We do not write the exact value
• This is because, in real life situations, the angle varies from molecule to molecule
♦ For example:
✰ In SO2, the angle is 119o
✰ In O3, the angle is 117o
• These are shown in figs.4.101 (a) and (b) respectively:
• Note that, there is a single bond each in SO2 and O3
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
We will write it in steps:
1. In AB2E2, there are 2 terminal atoms and 2 electron pairs
• So there is a total of 4 items
• These 4 items are distributed around A
2. Suppose that, all the 4 items are 'sticks'
• Then there will be 4 sticks around A
• We have already seen such a case in the previous sections
• It is the molecule AB4. It has 4 sticks around A
3. When there are 4 sticks around A, the shape is tetrahedral
• This is shown in the fig.4.102(a) below:
4. But actually in our present case, we do not have 4 sticks
• We have only 2 sticks and 2 lone pairs
• So from fig.4.102(a), we remove 2 sticks
• In the place of those 'removed sticks', we put lone pairs
• This is shown in fig.4.102(b)
♦ The sticks corresponding to Bi and Biv are removed
♦ Those 'removed sticks' are indicated by dashed blue lines
✰ The blue dashed lines help us to remember the positions of the lone pairs
♦ Bi and Biv are written inside dashed circles because, those 'B atoms' are not actually present in fig.b
5. Now there is a problem
• In the tetrahedral structure that we saw in AB4, we know that, the angle between any two bonds will be 109.5o
♦ That is., the angle between any two sticks will be 109.5o
• In our present case, we can write the '109.5o' between the two sticks: BiiA and BiiiA. Because, they are two well defined sticks
♦ But we cannot write the '109.5o' any where else
✰ That is.,
✰ We cannot write 109.5o between a dashed blue line and a blue line
✰ We cannot write 109.5o between the two dashed blue lines
■ The reason can be written in (iv) steps:
(i) The 'bonding electrons' are confined inside the stick
• So they occupy a definite space
(ii) But 'lone electrons' are not confined. They freely occupy a region. The region is an electron cloud
• So the dashed blue lines indicate clouds
(iii) We can easily measure an angle from a stick
• Because, a stick is well defined
(iv) But we cannot measure the angle from a cloud
• Because, the electron cloud does not have a well defined boundary
6. So there is no need to specify the 'angles in which one side is a blue dashed line'
■ We need to write only one angle: The angle between the two sticks
7. There is yet another problem:
• We had earlier obtained the 109.5o as follows:
The 4 sticks try to push each other as far away as possible, and they settle down with angles of '109.5'o between them
• But here there are no '4 sticks'. There are only '2 sticks' and 2 lone pairs
♦ However, since they are all electrons, they will all be pushing each other
♦ But the pushing (repulsion) are different
■ We can write:
The following three repulsion are different:
(i) Repulsion between the 2 sticks
(ii) Repulsion between a stick and a blue dashed line
(iii) Repulsion between the 2 blue dashed lines
So how do we finalize the angle?
8. The VSEPR theory helps us in this situation
It can be written in (iii) steps:
(i) The bond pairs are confined into sticks
(ii) But the lone pairs occupy a region
♦ As a result, the lone pairs require more space
(iii) Thus, the lone pairs are able to apply a 'greater repulsion'
• We can consider three types of repulsion: (a), (b) and (c)
(a) Repulsion between two bond pairs
♦ This is denoted as: bond pair-bond pair repulsion (bp-bp repulsion)
♦ This is the repulsion between two sticks
(b) Repulsion between a lone pair and a bond pair
♦ This is denoted as: lone pair-bond pair repulsion (lp-bp repulsion)
♦ This is the repulsion between a blue dashed line and a stick
(a) Repulsion between two lone pairs
♦ This is denoted as: lone pair-lone pair repulsion (lp-lp repulsion)
♦ This is the repulsion between two blue dashed lines
[Recall that, we have already seen (a) and (b) in the previous AB2E]
■ The VSEPR theory tells us that:
♦ (b) will be greater than (a)
♦ (c) will be greater than (b)
♦ So we have: (c) > (b) > (a)
✰ That is: (lp-lp repulsion) > (lp-bp repulsion) > (bp-bp repulsion)
9. Based on this, we can think about the angle
It can be written in (v) steps;
(i) The two sticks in fig.4.102(b), tries to maintain an angle of 109.5o between them
(ii) They try to maintain this angle, by using the bp-bp repulsion mentioned in (8) above
♦ This repulsion is indicated by the red double headed arrow in fig.4.103(a) below:
(iii) But the sticks are acted upon by other repulsion forces also. They are also shown in fig.4.103(a)
• The lp-bp repulsion is indicated by yellow double headed arrows
♦ There are four yellow arrows
✰ Readers are advised to recognize each of the yellow arrows individually
✰ Some of them are partially obstructed from view
✰ Even then, they must be fully recognized
• The lp-lp repulsion is indicated by a cyan double headed arrow
♦ There is only one such arrow
(iv) We see a clear and definite pattern here. The reader must be able to appreciate the pattern:
♦ The top head of the cyan arrow is exerting a push on two yellow arrows
✰ These yellow arrows in turn, are pushing the sticks from the top
♦ The bottom head of the cyan arrow is exerting a push on the other two yellow arrows
✰ These yellow arrows in turn, are pushing the sticks from the sides
(iv) According to the VSEPR theory, the cyan is stronger than yellow
♦ So the yellow arrows will be compressed
(v) The yellow arrows in turn, will compress the red arrow
♦ Because, according to the VSEPR theory, red is the weakest
(vi) Thus, the red is compressed from top as well as from the sides
♦ As a result, the angle between the sticks become less than 109.5o
♦ This is shown in fig.4.103(b)
♦ This fig.4.103(b) shows the final shape
10. Now we can write about the final shape
(i) The lone pairs influence the shape of the atoms but they are invisible
(ii) So the final shape is determined by the positions of the atoms
(iii) We have two 'B atoms' and one 'A atom'
• They do not lie on a straight line. So we call it: Bent structure
• Once we finalize the shape, we no longer need to show the blue dashed line. So it is not shown in fig.4.103(b)
11. Note that, even though it is a bent structure, it is not a 3D structure. It is a 2D structure
• The reason is obvious. It can be written in steps:
(i) A plane can be made to pass through any three given points (Details here)
(ii) So there will always be a plane which contains the two B atoms and the one Atom
(iii) So this bent molecule is always planar
12. The actual value of the angle:
• In the general case, we write that: The angle will be less than 109.5o
♦ We do not write the exact value
• This is because, in real life situations, the angle varies from molecule to molecule
♦ For example:
✰ In H2O, the angle is 104.5o
• This is shown in fig.4.104 below:
1. Let us recall the 'general forms' that we saw in the previous sections:
AB, AB2, AB3, AB4, AB5 and AB6
• These molecules do not have any lone pairs of electrons
(Note that, we are considering only 'those lone pairs which are possessed by the central atom')
2. When the molecules have lone pairs, we add 'Ei' to the general form
♦ The letter 'E' indicates the presence of lone pairs of electrons in the central atom
♦ The subscript 'i' indicates the 'number ' of lone pairs
3. Following are the 'general forms' of such molecules that we have to learn:
Case I: Number of B atoms = 2
(a) General form is: AB2E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by two B atoms
♦ A has one lone pair
(b) General form is: AB2E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by two B atoms
♦ A has two lone pairs
Case II: Number of B atoms = 3
(a) General form is: AB3E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by three B atoms
♦ A has one lone pair
(b) General form is: AB3E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by three B atoms
♦ A has two lone pairs
Case III: Number of B atoms = 4
(a) General form is: AB4E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by four B atoms
♦ A has one lone pair
(b) General form is: AB4E2
• In this case, i = 2
• So we can write:
♦ Central atom A is surrounded by four B atoms
♦ A has two lone pairs
Case IV: Number of B atoms = 5
(a) General form is: AB5E
• In this case, i = 1
• So we can write:
♦ Central atom A is surrounded by five B atoms
♦ A has one lone pair
• There are two important points that we have to always remember:
♦ It is not the 'number of electrons'
(ii) The 'lone pairs' are those electron pairs possessed by the central atom A
♦ The 'lone pairs' (if any), possessed by 'B atoms' are not considered in our present discussions
• At this stage, two questions arise in our minds:
Why is it that, there are no smaller cases like ABE and ABE2?
(ii) The largest case mentioned above (case IV with five B atoms) is AB5E
Why is it that, there is no larger cases like AB5E2?
• We will see the answers during the course of our discussions
• We now begin the discussion with Case I (a): AB2E
We will write it in steps:
1. In AB2E, there are 2 terminal atoms and 1 electron pair
• So there is a total of 3 items
• These 3 items are distributed around A
2. Suppose that all the three items are 'sticks'
• Then there will be 3 sticks around A
• We have already seen such a case in the previous sections
• It is the molecule AB3. It has 3 sticks around A
3. When there are 3 sticks around A, the shape is trigonal planar
• This is shown in the fig.4.99(a) below:
 |
| Fig.4.99 |
• We have only two sticks and one lone pair
• So from fig.4.99(a), we remove one stick
• In the place of that 'removed stick', we put a lone pair
• This is shown in fig.4.99(b)
♦ The 'removed stick' is indicated by a dashed blue line
✰ This blue dashed line help us to remember the position of the lone pair
5. Now there is a problem
• We can write the '120o' between the two bottom sticks. Because, they are two well defined sticks
• But we cannot write the '120o' on the left and right sides. The reason can be written in (iv) steps:
(i) The 'bonding electrons' are confined inside the stick
♦ This is because, they are shared by two atoms
♦ So they occupy a definite space
(ii) But 'lone electrons' are not confined. They freely occupy a region. The region is an electron cloud
(iii) We can easily measure an angle from a stick
♦ Because, a stick is well defined
(iv) But we cannot measure the angle from a cloud
♦ Because, the electron cloud does not have a well defined boundary
6. So we must remove the two '120o' angles on the left and right sides
• There is no need to specify those angles
• So the shape would be as shown in fig.4.99(c)
7. There is yet another problem:
• We had earlier obtained the 120o as follows:
The 3 sticks try to push each other as far away as possible, and they settle down with angles of '120o' between them
• But here there are no '3 sticks'. There are only '2 sticks' and a lone pair
♦ However, since they are all electrons, they will all be pushing each other
♦ But the pushing (repulsion) are different
■ We can write:
The following two repulsion are different:
(i) Repulsion between the 2 sticks
(ii) Repulsion between any one stick and a blue dashed line
So how do we finalize the angle?
8. The VSEPR theory helps us in this situation
It can be written in (iii) steps:
(i) The bond pairs are confined into sticks
(ii) But the lone pairs occupy a region
♦ As a result, the lone pairs require more space
(iii) Thus, the lone pairs are able to apply a 'greater repulsion'
• We can consider two types of repulsion: (a) and (b)
(a) Repulsion between two bond pairs
♦ This is denoted as: bond pair-bond pair repulsion (bp-bp repulsion)
♦ This is the repulsion between the two sticks
(b) Repulsion between a lone pair and a bond pair
♦ This is denoted as: lone pair-bond pair repulsion (lp-bp repulsion)
♦ This is the repulsion between the dashed blue line and a stick
■ The VSEPR theory tells us that, (b) will be greater than (a)
9. Based on this, we can think about the angle
• It can be written in (v) steps;
(i) The two sticks in fig.4.99(c), tries to maintain an angle of 120o between them
(ii) They try to maintain this angle, by using the bp-bp repulsion mentioned in (8) above
♦ This repulsion is indicated by the red double headed arrow in fig.4.100(a) below:
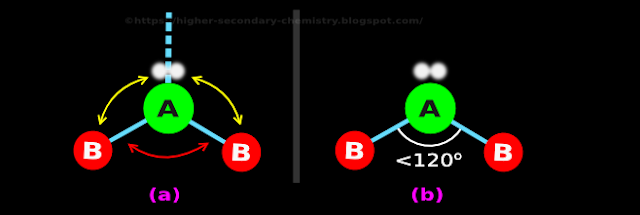 |
| Fig.4.100 |
• The left stick is acted upon by the repulsion from the lone pair
♦ This repulsion is indicated by the left yellow double headed arrow in fig.4.100(a)
• The right stick is also acted upon by the repulsion from the lone pair
♦ This repulsion is indicated by the right yellow double headed arrow in fig.4.100(a)
(iv) From (8), we know that, the yellow arrows are stronger than the red arrow
• So the two sticks will bend further down
(v) As a result, the angle between the sticks will become less than 120o
♦ This is shown in fig.4.100(b)
♦ This fig.4.100(b) shows the final shape
10. Now we can write about the final shape. It can be written in (iii) steps
(i) The lone pair influence the shape of the atoms but they are invisible
(ii) So the final shape is determined by the positions of the atoms
(iii) We have two 'B atoms' and one 'A atom'
♦ They do not lie on a straight line. So we call it: Bent structure
• Once we finalize the shape, we no longer need to show the blue dashed line. So it is not shown in fig.4.100(b)
11. Note that, even though it is a bent structure, it is not a 3D structure. It is a 2D structure
• The reason is obvious. It can be written in steps:
(i) A plane can be made to pass through any three given points (Details here)
(ii) So there will always be a plane which contains the two B atoms and the one A atom
(iii) So this bent molecule is always planar
12. The actual value of the angle:
• In the general case, we write that: The angle will be less than 120o
♦ We do not write the exact value
• This is because, in real life situations, the angle varies from molecule to molecule
♦ For example:
✰ In SO2, the angle is 119o
✰ In O3, the angle is 117o
• These are shown in figs.4.101 (a) and (b) respectively:
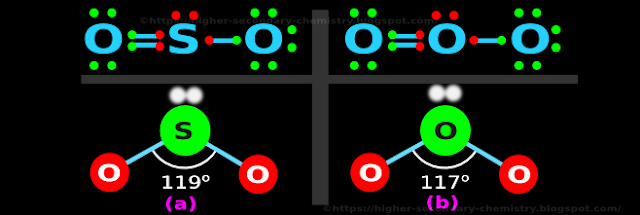 |
| Fig.4.101 |
♦ But in VSEPR theory,
✰ a double bond is considered as a 'single stick'
Next we consider Case I (b): AB2E2
1. In AB2E2, there are 2 terminal atoms and 2 electron pairs
• So there is a total of 4 items
• These 4 items are distributed around A
2. Suppose that, all the 4 items are 'sticks'
• Then there will be 4 sticks around A
• We have already seen such a case in the previous sections
• It is the molecule AB4. It has 4 sticks around A
3. When there are 4 sticks around A, the shape is tetrahedral
• This is shown in the fig.4.102(a) below:
 |
| Fig.4.102 |
• We have only 2 sticks and 2 lone pairs
• So from fig.4.102(a), we remove 2 sticks
• In the place of those 'removed sticks', we put lone pairs
• This is shown in fig.4.102(b)
♦ The sticks corresponding to Bi and Biv are removed
♦ Those 'removed sticks' are indicated by dashed blue lines
✰ The blue dashed lines help us to remember the positions of the lone pairs
♦ Bi and Biv are written inside dashed circles because, those 'B atoms' are not actually present in fig.b
5. Now there is a problem
• In the tetrahedral structure that we saw in AB4, we know that, the angle between any two bonds will be 109.5o
♦ That is., the angle between any two sticks will be 109.5o
• In our present case, we can write the '109.5o' between the two sticks: BiiA and BiiiA. Because, they are two well defined sticks
♦ But we cannot write the '109.5o' any where else
✰ That is.,
✰ We cannot write 109.5o between a dashed blue line and a blue line
✰ We cannot write 109.5o between the two dashed blue lines
■ The reason can be written in (iv) steps:
(i) The 'bonding electrons' are confined inside the stick
• So they occupy a definite space
(ii) But 'lone electrons' are not confined. They freely occupy a region. The region is an electron cloud
• So the dashed blue lines indicate clouds
(iii) We can easily measure an angle from a stick
• Because, a stick is well defined
(iv) But we cannot measure the angle from a cloud
• Because, the electron cloud does not have a well defined boundary
6. So there is no need to specify the 'angles in which one side is a blue dashed line'
■ We need to write only one angle: The angle between the two sticks
7. There is yet another problem:
• We had earlier obtained the 109.5o as follows:
The 4 sticks try to push each other as far away as possible, and they settle down with angles of '109.5'o between them
• But here there are no '4 sticks'. There are only '2 sticks' and 2 lone pairs
♦ However, since they are all electrons, they will all be pushing each other
♦ But the pushing (repulsion) are different
■ We can write:
The following three repulsion are different:
(i) Repulsion between the 2 sticks
(ii) Repulsion between a stick and a blue dashed line
(iii) Repulsion between the 2 blue dashed lines
So how do we finalize the angle?
8. The VSEPR theory helps us in this situation
It can be written in (iii) steps:
(i) The bond pairs are confined into sticks
(ii) But the lone pairs occupy a region
♦ As a result, the lone pairs require more space
(iii) Thus, the lone pairs are able to apply a 'greater repulsion'
• We can consider three types of repulsion: (a), (b) and (c)
(a) Repulsion between two bond pairs
♦ This is denoted as: bond pair-bond pair repulsion (bp-bp repulsion)
♦ This is the repulsion between two sticks
(b) Repulsion between a lone pair and a bond pair
♦ This is denoted as: lone pair-bond pair repulsion (lp-bp repulsion)
♦ This is the repulsion between a blue dashed line and a stick
(a) Repulsion between two lone pairs
♦ This is denoted as: lone pair-lone pair repulsion (lp-lp repulsion)
♦ This is the repulsion between two blue dashed lines
[Recall that, we have already seen (a) and (b) in the previous AB2E]
■ The VSEPR theory tells us that:
♦ (b) will be greater than (a)
♦ (c) will be greater than (b)
♦ So we have: (c) > (b) > (a)
✰ That is: (lp-lp repulsion) > (lp-bp repulsion) > (bp-bp repulsion)
9. Based on this, we can think about the angle
It can be written in (v) steps;
(i) The two sticks in fig.4.102(b), tries to maintain an angle of 109.5o between them
(ii) They try to maintain this angle, by using the bp-bp repulsion mentioned in (8) above
♦ This repulsion is indicated by the red double headed arrow in fig.4.103(a) below:
 |
| Fig.103 |
• The lp-bp repulsion is indicated by yellow double headed arrows
♦ There are four yellow arrows
✰ Readers are advised to recognize each of the yellow arrows individually
✰ Some of them are partially obstructed from view
✰ Even then, they must be fully recognized
• The lp-lp repulsion is indicated by a cyan double headed arrow
♦ There is only one such arrow
(iv) We see a clear and definite pattern here. The reader must be able to appreciate the pattern:
♦ The top head of the cyan arrow is exerting a push on two yellow arrows
✰ These yellow arrows in turn, are pushing the sticks from the top
♦ The bottom head of the cyan arrow is exerting a push on the other two yellow arrows
✰ These yellow arrows in turn, are pushing the sticks from the sides
(iv) According to the VSEPR theory, the cyan is stronger than yellow
♦ So the yellow arrows will be compressed
(v) The yellow arrows in turn, will compress the red arrow
♦ Because, according to the VSEPR theory, red is the weakest
(vi) Thus, the red is compressed from top as well as from the sides
♦ As a result, the angle between the sticks become less than 109.5o
♦ This is shown in fig.4.103(b)
♦ This fig.4.103(b) shows the final shape
10. Now we can write about the final shape
(i) The lone pairs influence the shape of the atoms but they are invisible
(ii) So the final shape is determined by the positions of the atoms
(iii) We have two 'B atoms' and one 'A atom'
• They do not lie on a straight line. So we call it: Bent structure
• Once we finalize the shape, we no longer need to show the blue dashed line. So it is not shown in fig.4.103(b)
11. Note that, even though it is a bent structure, it is not a 3D structure. It is a 2D structure
• The reason is obvious. It can be written in steps:
(i) A plane can be made to pass through any three given points (Details here)
(ii) So there will always be a plane which contains the two B atoms and the one Atom
(iii) So this bent molecule is always planar
12. The actual value of the angle:
• In the general case, we write that: The angle will be less than 109.5o
♦ We do not write the exact value
• This is because, in real life situations, the angle varies from molecule to molecule
♦ For example:
✰ In H2O, the angle is 104.5o
• This is shown in fig.4.104 below:
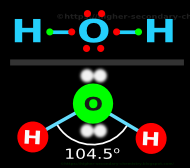 |
| Fig.4.104 |
• We will see case II in the next section
No comments:
Post a Comment