In the previous section 3.6, we completed a discussion on periodic trends in ionic radius. In this section, we will see periodic trends in ionization enthalpy
1. We know that, in every atom, the electrons are held in their orbitals around the nucleus
• We can call it an atom only if all the electrons are present
• If any of the electrons are lost, it can no longer be called an atom. It will be called an ion (cation)
2. So when we deal with an atom, we need to know these:
• Does the atom has the tendency to readily lose the electrons?
OR
• Does the atom has the tendency to keep the electrons tightly bound to itself?
■ To answer those questions, we introduce a new property called ionization enthalpy
3. Ionization enthalpy is an energy
It is measured using an experiment. That experiment can be explained in 3 steps:
(i) We want to measure the ionization enthalpy of an element
• Take one atom of that element
♦ Denote this one atom as X
(ii) Remove the outermost electron from X
• Note down the energy required for the removal
(iii) The energy noted in step 2, is the energy required for one atom X
• Calculate the energy required for one mole (6.023 × 1023 nos. of X atoms)
(This can be done by multiplying the energy value by 6.023 × 103)
■ The energy required (in kilo joules) for one mole is recorded as the ionization enthalpy
♦ It’s symbol is ΔH
♦ It’s unit is kJ/mole
(We will see the practical method for carrying out this experiment in higher classes)
4. For carrying out the experiment, the one atom X must satisfy 3 conditions:
(i) X must be in the gaseous state
(ii) X must be isolated from all other atoms
(iii) X must be in the ground state
5. Let us see the reason for imposing the 3 conditions:
(i) We want to pick just 'one atom of the element' for doing the experiment
• This is possible only when the element is in the gaseous state
♦ Recall that, in the gaseous state, the atoms will be at a greater distances apart
• So we impose the condition that, the atom X should be in the gaseous state
(ii) If the X is near other atoms, inter molecular forces will be acting
• If those inter molecular forces are acting, our experiment will not give correct values
• So we impose the condition that, the atom X should be isolated from other atoms
(iii) While performing the experiment, all the electrons of X must be in their original orbitals
• If they are in higher orbitals, it would mean that, the electrons already has some 'extra energy'
• In such a situation, the experiment will not give correct values
• So we impose the condition that, the atom X should be in the ground state
6. Now we can write the definition for ionization enthalpy:
Ionization enthalpy is the energy required to remove an electron from an isolated gaseous atom (X) in it’s ground state
7. Ionization enthalpy can be classified as:
(i) First ionization enthalpy is the energy required to remove the ‘most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X(g)\longrightarrow X^+(g)\,+e^-}}$
(ii) Second ionization enthalpy is the energy required to remove the ‘second most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X^+(g)\longrightarrow X^{2+}(g)\,+e^-}}$
(iii) Third ionization enthalpy is the energy required to remove the ‘third most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X^{2+}(g)\longrightarrow X^{3+}(g)\,+e^-}}$
8. The second ionization enthalpy will be greater than the first ionization enthalpy
• The reason can be written in 3 steps:
(i) When the first electron is removed, the remaining electrons will be held more tightly by the nucleus
(ii) So it is more difficult to remove a second electron
(iii) That means, more energy is required to remove the second electron
9. In the same way:
• Third ionization enthalpy will be greater than the second ionization enthalpy
• Fourth ionization enthalpy will be greater than the third ionization enthalpy
• so on . . .
10. Sometimes we will be given just ‘ionization enthalpy’
• There will not be any prefix: first, second, third etc.,
■ Then it implies that, it is the first ionization enthalpy
11. Every element has it’s own unique value of ionization enthalpy
• For example, the ionization enthalpy of Li is 520.2 kJ/mol
• A complete list can be seen here
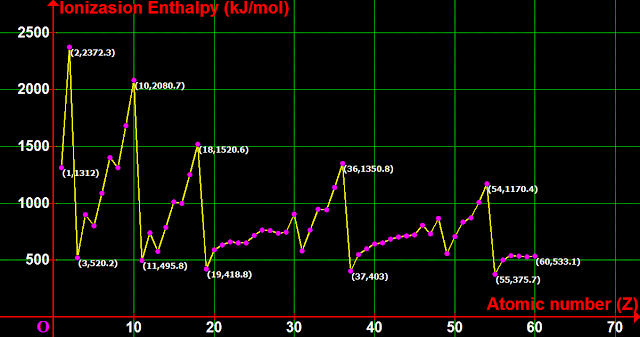
1. Consider the graph shown in fig.3.7 below
♦ Atomic number Z is plotted along the x-axis
♦ ΔH is plotted along the y-axis
• The ΔH values of the elements are plotted in serial order of atomic number Z
2. We see that, the ΔH of 2He (2372.3 kJ/mol) is higher than the ΔH of 1H (1312 kJ/mol)
• This is expected. We can write the explanation in 3 steps:
(i) In 1H, the outermost electron is pulled by one proton
• In 2He, each of the outermost electrons are pulled by two protons
(ii) Mathematically, we can write:
• $\mathbf\small{F_H\propto \left[1e^2\right]}$
♦ Where $\mathbf\small{F_H}$ is the force with which the electron in 1H is pulled by it's nucleus
♦ '$\mathbf\small{\propto}$' stands for 'is proportional to'
• $\mathbf\small{F_{He}\propto \left[2e^2\right]}$
♦ Where $\mathbf\small{F_{He}}$ is the force with which the electron in 2He is pulled by it's nucleus
(iii) We see that, $\mathbf\small{F_{He}}$ is greater than $\mathbf\small{F_H}$
• That means, the electrons of 2He are pulled more tightly by the nucleus
• So, when compared to hydrogen, it is more difficult to remove the outermost electron of helium
• In other words 2He has a greater ΔH value than 1H
3. After 2He, we proceed to the next element which is: 3Li
• We see that, there is a sudden drop in the ΔH value. Li is far below He
• This is not expected because, Li has one proton more than He
4. So what is the reason for the drop?
• We can write the explanation in 3 steps:
(i) The fig.3.8(b) below shows the orbital diagram of Li
• The last electron is present in the 2s orbital
(ii) We see that, the 1s orbital is completely filled
• This completely filled 1s orbital (the helium core) is present in between the last electron and the nucleus
(iii) So the 1s electrons form a shield (screen) between the last electron and the nucleus
• As a result, the outermost electron will not experience the full force from the nucleus
• So it is easier to remove the last electron
• In other words, Li will have a lower ΔH value
5. A similar condition occurs in the case of Na
• It’s orbital diagram is shown in fig.3.8(c)
• The neon core acts as a shield between the last electron and the nucleus
• As a result, the outermost electron of Na will not experience the full force from the nucleus
• So it is easier to remove that outermost electron
• Thus, the ΔH of Na will also be very low
6. Similar situation occurs in the case of K, Rb, Cs and Fr also
♦ K has the 4s1 electron outside the [Ar] core
♦ Rb has the 5s1 electron outside the [Kr] core
♦ Cs has the 6s1 electron outside the [Xe] core
♦ Fr has the 7s1 electron outside the [Rn] core
■ So we can write:
The elements Li, Na, K, Rb, Cs and Fr have very low ΔH values
• Note that, these elements form the group 1 of the periodic table
■ So we can write:
The group 1 elements form the minima of the graph in fig.3.7
7. So we got an advantage:
• While analyzing the reason for the ‘low ΔH value of Li’ in step (3), we came to know why ‘the group 1 elements form the minima’ of the graph
8. The low ΔH values of group 1 elements can be related to their high reactivities
• These elements readily take part in chemical reactions
• This is because, they lose their outermost electron easily
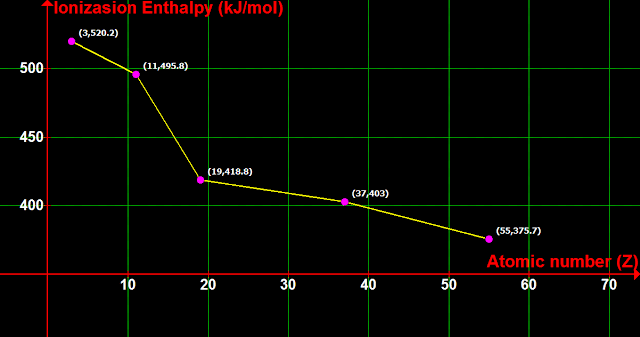
■ Which one among them has the highest reactivity?
• The answer can be written in steps:
(i) The minima in fig.3.7 can be taken out separately
(ii) A graph can be plotted using those 'taken out' values:
• We see that there is a decreasing trend:
♦ 11Na has a lower ΔH than 3Li
♦ 19K has a lower ΔH than 11Na
♦ 37Rb has a lower ΔH than 19K
♦ 55Cs has a lower ΔH than 37Rb
• All these elements belong to the same group, which is: group 1 (alkali metals)
(iii) Following this trend, 87Fr will have the lowest ΔH, and hence the highest reactivity
9. After Li, we proceed to the next element which is: Be
• In fig.3.7, we see that, Be has a higher ΔH than Li
• This will become more clear if we enlarge the left portion of the graph in fig.3.7
• Enlargement can be achieved if we decide to discard the atomic numbers beyond 10
• Then the details from atomic numbers 3 to 10 can be drawn in a larger space, and we can add more details
• Such a graph is shown in fig.3.10 below:
♦ 3Li has 520.2 kJ/mol
♦ 4Be has 899.5 kJ/mol
10. It is clear that, ΔH of Be is greater
• This is easy to explain. We can do it in 5 steps:
(i) The ΔH depends on two factors:
♦ The pull from the nucleus
♦ The shielding effect by the core
(ii) We can put this in a mathematical form for both Li and Be:
♦ The ΔH of Li $\mathbf\small{\propto}$ [Pull from Li nucleus – shielding by 'core in Li atom']
♦ The ΔH of Be $\mathbf\small{\propto}$ [Pull from Be nucleus – shielding by 'core in Be atom']
(iii) The ‘shielding by core in Li atom’ is same as ‘shielding by core in Be atom’
• Because, both Li and Be have the same [He] core
• So the 'quantity subtracted' is same for both the equations in (ii)
(iv) ‘Pull from Be nucleus’ will be greater than the ‘pull from Li nucleus’
• This is because, Be has one proton more than Li
• So the 'quantity from which subtraction is done' is greater in the second equation in (ii)
(v) So we can see that 'ΔH of Be' will be greater than the 'ΔH of Li'
(vi) This will become even more clear if we make a bar chart as shown in fig.3.11 below:
• We calculate two items:
♦ For ΔH of Li: Subtract cyan from yellow
♦ For ΔH of Be: Subtract cyan from magenta
• Obviously, the second result will be greater
10. Now we proceed to the next element after Be, which is: B
• We see that, B has a lower ΔH than Be
♦ 4Be has 899.5 kJ/mol
♦ 5B has 800.6 kJ/mol
11. This is not expected
• B has one proton more than Be. So the electrons in B must be held more tightly than in Be
• Consequently, the ΔH of B must be greater than Be. But this is not what we see from the graph
• So it is an anomaly
('Anomaly' means: Something that deviates from what is standard, normal, or expected. See dictionary meaning here)
12. The explanation can be written in steps:
(i) The orbital diagram of B is shown in fig.3.8(d)
• Comparing it with fig.3.8(c), we can see that:
♦ For Be, the electron which is to be removed, is in the 2p orbital
♦ For B, the electron which is to be removed, is in the 2s orbital
• Both are in the second main-shell
(ii) Here we make a comparison between two items:
♦ The 2s orbital
♦ The 2p orbital
• Scientists have proved that, the 2s orbital has 'greater penetration' when compared to the 2p orbital
♦ That is, the 2s orbital cloud is ‘closer to the nucleus’ when compared to the 2p orbital cloud
(iii) Now, both the '2s in Be' and '2p in B' will be experiencing the same shielding
♦ Because, in both cases, the shielding is caused by the [He] core
(iv) But we see that, the 2s has greater penetration than 2p
• ‘Greater penetration’ results in, ‘lesser shielding’
• That means, the 2s experience a lesser shielding than 2p
• This is same as:
♦ 2p experience a greater shielding than 2s
♦ So it is easier to ‘remove the 2p electron’ than to ‘remove the 2s electron’
(v) Mathematically we can write:
• The ΔH of Be $\mathbf\small{\propto}$ [Pull from Be nucleus – shielding by 'core of Be atom']
• The ΔH of B $\mathbf\small{\propto}$ [Pull from B nucleus – shielding by 'core of B atom']
(vi) In (v), 'Pull from B nucleus' is higher than 'Pull from Be nucleus'
• So we would expect 'ΔH of B' to be higher than 'ΔH of Be'
(vii) In (v) 'core of Be atom' is same as 'core of B atom', which is the [He] core
(viii) 'shielding by core of Be atom' is very less than the 'shielding by core of B atom' because, Be has greater penetration
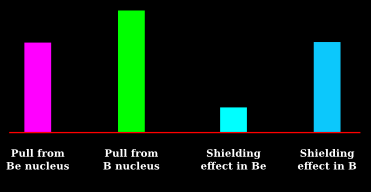
(ix) So the net result is that, 'ΔH of B' is a little lower than 'ΔH of Be'
(x) This will become even more clear if we make a bar chart as shown in fig.3.11 below:
• We calculate two items:
♦ For ΔH of Be: Subtract cyan from magenta
♦ For ΔH of B: Subtract blue from green
• Green is larger than magenta
♦ Even then, (green - blue) will be smaller than (magenta - cyan)
♦ This is because, cyan is much smaller than blue. The reason is written in (viii) above
• So ΔH of B is smaller than ΔH of Be
13. Now we proceed to the next element after B, which is: C
• We see that, C has a higher ΔH than Be and B
♦ 4Be has 899.5 kJ/mol
♦ 5B has 800.6 kJ/mol
♦ 6C has 1086.5 kJ/mol
14. So the trend is back
■ That is., with increasing atomic number, the ΔH is increasing
• This is because, with the addition of one more proton, the pull towards the nucleus increases
• In the case of 6C, the pull increases to such a high value that, the shielding effect is out weighted
15. This trend continues upto 10Ne
• However, there is one more anomaly at 8O
♦ 7N has 1403.3 kJ/mol
♦ 8O has 1313.9 kJ/mol
• Even after the addition of one more proton, the ΔH of O has decreased a bit
16. The explanation can be written in 3 steps:
(i) Fig.3.7(e) shows the orbital diagram of N
• We see that, all the 2p orbitals are half-filled
• This arises due to Hund's rule. We have already seen it in the previous chapter
(ii) Due to the half-filled orbitals, the N has some extra stability
• It is very difficult to remove an electron from the N atom
(iii) But in O, one of the 2p orbitals have two electrons
• This results in an increased repulsion between electrons
• So it is easier (when compared to N) to remove the electron
• Thus the 'ΔH value of O' is slightly lower than the 'ΔH value of N'
17. So we have seen the periodic trend in ionization enthalpy (ΔH) from 3Li to 10Ne
• This completes the 2nd period
18. The 3rd period starts from 11Na and ends at 18Ar
• In the fig.3.7, compare the following two items:
♦ The graph from 3Li to 10Ne
♦ The graph from 11Na to 18Ar
• We see that, both the graphs have similar shapes
• That means, the same trends can be seen from 11Na to 18Ar also
Solved example 3.11
The first ionization enthalpy (∆H) values of the third period elements, Na, Mg and Si are respectively 496, 737 and 786 kJ/mol. Predict whether the first ∆H value for Al will be more close to 575 or 760 kJ/mol ? Justify your answer
Solution:
1. The order of elements is: Na, Mg, Al, Si
♦ The electronic configuration of Mg is: 1s22s22p63s2
♦ The electronic configuration of Al is: 1s22s22p63s23p1
2. The core (in both the cases) is the first 3 items: [1s22s22p6]
♦ In Mg, this core shields the 3s2 electrons from the nucleus
♦ In Al, this core shields the (3s2 and 3p1) electrons from the nucleus
3. But the 3s has greater penetration than 3p
• So the 3s in Mg has lesser shielding effect than 3p
• So it is easier to remove the 3p electrons than 3s electrons
• Thus the ΔH of Al will be less than the ΔH of Mg
4. Given that, ΔH of Mg is 737 kJ/mol
• The possible values given for Al are 575 and 760
• Out of these, only 575 is less than 737
■ So we can write:
∆H value for Al will be more close to 575 kJ/mol
Solved example 3.12
Energy of an electron in the ground state of the hydrogen atom is -2.18 × 10-18 J. Calculate the ionization enthalpy of atomic hydrogen in terms of J/mol
Hint: Apply the idea of mole concept to derive the answer
Solution:
1. Given that the energy of one electron in the ground state of the hydrogen atom = -2.18 × 10-18 J
2. So, if we supply this much energy, that electron will get removed from the atom
• That means, to remove one electron in the ground state of the hydrogen atom, we have to supply 2.18 × 10-18 J of energy
3. This is the energy required to remove the electron from one atom
• So for 6.023 × 10-18 nos. of atoms, we have to supply (2.18 × 10-18 × 6.023 × 1023) = 1.313 × 106 J of energy
4. But the 'energy required to remove the electron from one mole of atoms' is ionization enthalpy
■ So we can write:
The ionization enthalpy of atomic hydrogen in terms of J/mol is 1.313 × 106 J/mol
Solved example 3.13
Among the second period elements the actual ionization enthalpies are in the order Li < B < Be < C < O < N < F < Ne.
Explain why
(i) Be has higher ∆H than B
(ii) O has lower ∆H than N and F?
Solution:
Part (i):
See steps (10) to (12) above
Part (ii):
See steps (15) and (16) above
Solved example 3.14
How would you explain the fact that the first ionization enthalpy of sodium is lower than that of magnesium but its second ionization enthalpy is higher than that of magnesium?
Solution:
1. Let us write the electronic configurations:
• The electronic configuration of Na is [1s22s22p6]3s1
• The electronic configuration of Mg is [1s22s22p6]3s2
2. In both cases, the first electron will be removed from the 3s orbital
• The Mg has greater number of protons
• So it's electrons will be held more tightly
• Consequently, it's ΔH value will be higher than that of Na
3. Once the first electrons are removed,
• The electronic configuration of Na+ will be [1s22s22p6]
• The electronic configuration of Mg+ will be [1s22s22p6]3s1
4. We see that,
• In Na+, there is no third main-shell
♦ The configuration is same as that of the noble gas Ne
♦ It is very difficult to remove an electron from a noble gas configuration
• In Mg+, the last electron is present in the third main-shell
♦ That electron can be removed easily to attain noble gas configuration
5. That means,
• In Na+, the last electron is more tightly held to the nucleus than in Mg+
• So the second ionization enthalpy of Na will be higher than the second ionization enthalpy of Mg
Solved example 3.15
What are the various factors due to which the ionization enthalpy of the main group elements tends to decrease down a group?
Solution:
We can write 2 factors:
1. Increasing number of main-shells. This can be explained in 4 steps:
(i) When we move down the group, the number of main-shells increases
(ii) So the valence electrons are not tightly held to the nucleus
(iii) As a result, the valence electrons can be easily removed from the atom
(iv) In other words, the ΔH values become lower and lower
2. Increasing shielding effect. This can be explained in 6 steps:
(i) When we move down the group, the number of main-shells increases
(ii) So the number of inner shells also increases as we go down the group
(iii) This increases the shielding effect
• That is., when we move down the group, the valence electrons are more effectively shielded from the nucleus
(iv) So the valence electrons are not tightly held to the nucleus
(v) As a result, the valence electrons can be easily removed from the atom
(vi) In other words, the ΔH values become lower and lower
1. We know that, in every atom, the electrons are held in their orbitals around the nucleus
• We can call it an atom only if all the electrons are present
• If any of the electrons are lost, it can no longer be called an atom. It will be called an ion (cation)
2. So when we deal with an atom, we need to know these:
• Does the atom has the tendency to readily lose the electrons?
OR
• Does the atom has the tendency to keep the electrons tightly bound to itself?
■ To answer those questions, we introduce a new property called ionization enthalpy
3. Ionization enthalpy is an energy
It is measured using an experiment. That experiment can be explained in 3 steps:
(i) We want to measure the ionization enthalpy of an element
• Take one atom of that element
♦ Denote this one atom as X
(ii) Remove the outermost electron from X
• Note down the energy required for the removal
(iii) The energy noted in step 2, is the energy required for one atom X
• Calculate the energy required for one mole (6.023 × 1023 nos. of X atoms)
(This can be done by multiplying the energy value by 6.023 × 103)
■ The energy required (in kilo joules) for one mole is recorded as the ionization enthalpy
♦ It’s symbol is ΔH
♦ It’s unit is kJ/mole
(We will see the practical method for carrying out this experiment in higher classes)
4. For carrying out the experiment, the one atom X must satisfy 3 conditions:
(i) X must be in the gaseous state
(ii) X must be isolated from all other atoms
(iii) X must be in the ground state
5. Let us see the reason for imposing the 3 conditions:
(i) We want to pick just 'one atom of the element' for doing the experiment
• This is possible only when the element is in the gaseous state
♦ Recall that, in the gaseous state, the atoms will be at a greater distances apart
• So we impose the condition that, the atom X should be in the gaseous state
(ii) If the X is near other atoms, inter molecular forces will be acting
• If those inter molecular forces are acting, our experiment will not give correct values
• So we impose the condition that, the atom X should be isolated from other atoms
(iii) While performing the experiment, all the electrons of X must be in their original orbitals
• If they are in higher orbitals, it would mean that, the electrons already has some 'extra energy'
• In such a situation, the experiment will not give correct values
• So we impose the condition that, the atom X should be in the ground state
6. Now we can write the definition for ionization enthalpy:
Ionization enthalpy is the energy required to remove an electron from an isolated gaseous atom (X) in it’s ground state
7. Ionization enthalpy can be classified as:
(i) First ionization enthalpy is the energy required to remove the ‘most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X(g)\longrightarrow X^+(g)\,+e^-}}$
(ii) Second ionization enthalpy is the energy required to remove the ‘second most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X^+(g)\longrightarrow X^{2+}(g)\,+e^-}}$
(iii) Third ionization enthalpy is the energy required to remove the ‘third most loosely bound electron’ from X
• In other words, it is the energy required to carry out the reaction given below:
$\mathbf\small{\rm{X^{2+}(g)\longrightarrow X^{3+}(g)\,+e^-}}$
8. The second ionization enthalpy will be greater than the first ionization enthalpy
• The reason can be written in 3 steps:
(i) When the first electron is removed, the remaining electrons will be held more tightly by the nucleus
(ii) So it is more difficult to remove a second electron
(iii) That means, more energy is required to remove the second electron
9. In the same way:
• Third ionization enthalpy will be greater than the second ionization enthalpy
• Fourth ionization enthalpy will be greater than the third ionization enthalpy
• so on . . .
10. Sometimes we will be given just ‘ionization enthalpy’
• There will not be any prefix: first, second, third etc.,
■ Then it implies that, it is the first ionization enthalpy
11. Every element has it’s own unique value of ionization enthalpy
• For example, the ionization enthalpy of Li is 520.2 kJ/mol
• A complete list can be seen here
So now we know the basics of ionization enthalpy (ΔH). We can start the discussion on it’s periodic trends
♦ Atomic number Z is plotted along the x-axis
♦ ΔH is plotted along the y-axis
• The ΔH values of the elements are plotted in serial order of atomic number Z
 |
| Fig.3.7 |
• This is expected. We can write the explanation in 3 steps:
(i) In 1H, the outermost electron is pulled by one proton
• In 2He, each of the outermost electrons are pulled by two protons
(ii) Mathematically, we can write:
• $\mathbf\small{F_H\propto \left[1e^2\right]}$
♦ Where $\mathbf\small{F_H}$ is the force with which the electron in 1H is pulled by it's nucleus
♦ '$\mathbf\small{\propto}$' stands for 'is proportional to'
• $\mathbf\small{F_{He}\propto \left[2e^2\right]}$
♦ Where $\mathbf\small{F_{He}}$ is the force with which the electron in 2He is pulled by it's nucleus
(iii) We see that, $\mathbf\small{F_{He}}$ is greater than $\mathbf\small{F_H}$
• That means, the electrons of 2He are pulled more tightly by the nucleus
• So, when compared to hydrogen, it is more difficult to remove the outermost electron of helium
• In other words 2He has a greater ΔH value than 1H
3. After 2He, we proceed to the next element which is: 3Li
• We see that, there is a sudden drop in the ΔH value. Li is far below He
• This is not expected because, Li has one proton more than He
4. So what is the reason for the drop?
• We can write the explanation in 3 steps:
(i) The fig.3.8(b) below shows the orbital diagram of Li
• The last electron is present in the 2s orbital
 |
| Fig.3.8 |
• This completely filled 1s orbital (the helium core) is present in between the last electron and the nucleus
(iii) So the 1s electrons form a shield (screen) between the last electron and the nucleus
• As a result, the outermost electron will not experience the full force from the nucleus
• So it is easier to remove the last electron
• In other words, Li will have a lower ΔH value
5. A similar condition occurs in the case of Na
• It’s orbital diagram is shown in fig.3.8(c)
• The neon core acts as a shield between the last electron and the nucleus
• As a result, the outermost electron of Na will not experience the full force from the nucleus
• So it is easier to remove that outermost electron
• Thus, the ΔH of Na will also be very low
6. Similar situation occurs in the case of K, Rb, Cs and Fr also
♦ K has the 4s1 electron outside the [Ar] core
♦ Rb has the 5s1 electron outside the [Kr] core
♦ Cs has the 6s1 electron outside the [Xe] core
♦ Fr has the 7s1 electron outside the [Rn] core
■ So we can write:
The elements Li, Na, K, Rb, Cs and Fr have very low ΔH values
• Note that, these elements form the group 1 of the periodic table
■ So we can write:
The group 1 elements form the minima of the graph in fig.3.7
7. So we got an advantage:
• While analyzing the reason for the ‘low ΔH value of Li’ in step (3), we came to know why ‘the group 1 elements form the minima’ of the graph
8. The low ΔH values of group 1 elements can be related to their high reactivities
• These elements readily take part in chemical reactions
• This is because, they lose their outermost electron easily
■ Which one among them has the highest reactivity?
• The answer can be written in steps:
(i) The minima in fig.3.7 can be taken out separately
(ii) A graph can be plotted using those 'taken out' values:
 |
| Fig.3.9 |
♦ 11Na has a lower ΔH than 3Li
♦ 19K has a lower ΔH than 11Na
♦ 37Rb has a lower ΔH than 19K
♦ 55Cs has a lower ΔH than 37Rb
• All these elements belong to the same group, which is: group 1 (alkali metals)
(iii) Following this trend, 87Fr will have the lowest ΔH, and hence the highest reactivity
9. After Li, we proceed to the next element which is: Be
• In fig.3.7, we see that, Be has a higher ΔH than Li
• This will become more clear if we enlarge the left portion of the graph in fig.3.7
• Enlargement can be achieved if we decide to discard the atomic numbers beyond 10
• Then the details from atomic numbers 3 to 10 can be drawn in a larger space, and we can add more details
• Such a graph is shown in fig.3.10 below:
 |
| Fig.3.10 |
♦ 4Be has 899.5 kJ/mol
10. It is clear that, ΔH of Be is greater
• This is easy to explain. We can do it in 5 steps:
(i) The ΔH depends on two factors:
♦ The pull from the nucleus
♦ The shielding effect by the core
(ii) We can put this in a mathematical form for both Li and Be:
♦ The ΔH of Li $\mathbf\small{\propto}$ [Pull from Li nucleus – shielding by 'core in Li atom']
♦ The ΔH of Be $\mathbf\small{\propto}$ [Pull from Be nucleus – shielding by 'core in Be atom']
(iii) The ‘shielding by core in Li atom’ is same as ‘shielding by core in Be atom’
• Because, both Li and Be have the same [He] core
• So the 'quantity subtracted' is same for both the equations in (ii)
(iv) ‘Pull from Be nucleus’ will be greater than the ‘pull from Li nucleus’
• This is because, Be has one proton more than Li
• So the 'quantity from which subtraction is done' is greater in the second equation in (ii)
(v) So we can see that 'ΔH of Be' will be greater than the 'ΔH of Li'
(vi) This will become even more clear if we make a bar chart as shown in fig.3.11 below:
 |
| Fig.3.11 |
• We calculate two items:
♦ For ΔH of Li: Subtract cyan from yellow
♦ For ΔH of Be: Subtract cyan from magenta
• Obviously, the second result will be greater
10. Now we proceed to the next element after Be, which is: B
• We see that, B has a lower ΔH than Be
♦ 4Be has 899.5 kJ/mol
♦ 5B has 800.6 kJ/mol
11. This is not expected
• B has one proton more than Be. So the electrons in B must be held more tightly than in Be
• Consequently, the ΔH of B must be greater than Be. But this is not what we see from the graph
• So it is an anomaly
('Anomaly' means: Something that deviates from what is standard, normal, or expected. See dictionary meaning here)
12. The explanation can be written in steps:
(i) The orbital diagram of B is shown in fig.3.8(d)
• Comparing it with fig.3.8(c), we can see that:
♦ For Be, the electron which is to be removed, is in the 2p orbital
♦ For B, the electron which is to be removed, is in the 2s orbital
• Both are in the second main-shell
(ii) Here we make a comparison between two items:
♦ The 2s orbital
♦ The 2p orbital
• Scientists have proved that, the 2s orbital has 'greater penetration' when compared to the 2p orbital
♦ That is, the 2s orbital cloud is ‘closer to the nucleus’ when compared to the 2p orbital cloud
(iii) Now, both the '2s in Be' and '2p in B' will be experiencing the same shielding
♦ Because, in both cases, the shielding is caused by the [He] core
(iv) But we see that, the 2s has greater penetration than 2p
• ‘Greater penetration’ results in, ‘lesser shielding’
• That means, the 2s experience a lesser shielding than 2p
• This is same as:
♦ 2p experience a greater shielding than 2s
♦ So it is easier to ‘remove the 2p electron’ than to ‘remove the 2s electron’
(v) Mathematically we can write:
• The ΔH of Be $\mathbf\small{\propto}$ [Pull from Be nucleus – shielding by 'core of Be atom']
• The ΔH of B $\mathbf\small{\propto}$ [Pull from B nucleus – shielding by 'core of B atom']
(vi) In (v), 'Pull from B nucleus' is higher than 'Pull from Be nucleus'
• So we would expect 'ΔH of B' to be higher than 'ΔH of Be'
(vii) In (v) 'core of Be atom' is same as 'core of B atom', which is the [He] core
(viii) 'shielding by core of Be atom' is very less than the 'shielding by core of B atom' because, Be has greater penetration
(ix) So the net result is that, 'ΔH of B' is a little lower than 'ΔH of Be'
(x) This will become even more clear if we make a bar chart as shown in fig.3.11 below:
 |
| Fig.3.12 |
• We calculate two items:
♦ For ΔH of Be: Subtract cyan from magenta
♦ For ΔH of B: Subtract blue from green
• Green is larger than magenta
♦ Even then, (green - blue) will be smaller than (magenta - cyan)
♦ This is because, cyan is much smaller than blue. The reason is written in (viii) above
• So ΔH of B is smaller than ΔH of Be
13. Now we proceed to the next element after B, which is: C
• We see that, C has a higher ΔH than Be and B
♦ 4Be has 899.5 kJ/mol
♦ 5B has 800.6 kJ/mol
♦ 6C has 1086.5 kJ/mol
14. So the trend is back
■ That is., with increasing atomic number, the ΔH is increasing
• This is because, with the addition of one more proton, the pull towards the nucleus increases
• In the case of 6C, the pull increases to such a high value that, the shielding effect is out weighted
15. This trend continues upto 10Ne
• However, there is one more anomaly at 8O
♦ 7N has 1403.3 kJ/mol
♦ 8O has 1313.9 kJ/mol
• Even after the addition of one more proton, the ΔH of O has decreased a bit
16. The explanation can be written in 3 steps:
(i) Fig.3.7(e) shows the orbital diagram of N
• We see that, all the 2p orbitals are half-filled
• This arises due to Hund's rule. We have already seen it in the previous chapter
(ii) Due to the half-filled orbitals, the N has some extra stability
• It is very difficult to remove an electron from the N atom
(iii) But in O, one of the 2p orbitals have two electrons
• This results in an increased repulsion between electrons
• So it is easier (when compared to N) to remove the electron
• Thus the 'ΔH value of O' is slightly lower than the 'ΔH value of N'
17. So we have seen the periodic trend in ionization enthalpy (ΔH) from 3Li to 10Ne
• This completes the 2nd period
18. The 3rd period starts from 11Na and ends at 18Ar
• In the fig.3.7, compare the following two items:
♦ The graph from 3Li to 10Ne
♦ The graph from 11Na to 18Ar
• We see that, both the graphs have similar shapes
• That means, the same trends can be seen from 11Na to 18Ar also
We will now see some solved examples
The first ionization enthalpy (∆H) values of the third period elements, Na, Mg and Si are respectively 496, 737 and 786 kJ/mol. Predict whether the first ∆H value for Al will be more close to 575 or 760 kJ/mol ? Justify your answer
Solution:
1. The order of elements is: Na, Mg, Al, Si
♦ The electronic configuration of Mg is: 1s22s22p63s2
♦ The electronic configuration of Al is: 1s22s22p63s23p1
2. The core (in both the cases) is the first 3 items: [1s22s22p6]
♦ In Mg, this core shields the 3s2 electrons from the nucleus
♦ In Al, this core shields the (3s2 and 3p1) electrons from the nucleus
3. But the 3s has greater penetration than 3p
• So the 3s in Mg has lesser shielding effect than 3p
• So it is easier to remove the 3p electrons than 3s electrons
• Thus the ΔH of Al will be less than the ΔH of Mg
4. Given that, ΔH of Mg is 737 kJ/mol
• The possible values given for Al are 575 and 760
• Out of these, only 575 is less than 737
■ So we can write:
∆H value for Al will be more close to 575 kJ/mol
Solved example 3.12
Energy of an electron in the ground state of the hydrogen atom is -2.18 × 10-18 J. Calculate the ionization enthalpy of atomic hydrogen in terms of J/mol
Hint: Apply the idea of mole concept to derive the answer
Solution:
1. Given that the energy of one electron in the ground state of the hydrogen atom = -2.18 × 10-18 J
2. So, if we supply this much energy, that electron will get removed from the atom
• That means, to remove one electron in the ground state of the hydrogen atom, we have to supply 2.18 × 10-18 J of energy
3. This is the energy required to remove the electron from one atom
• So for 6.023 × 10-18 nos. of atoms, we have to supply (2.18 × 10-18 × 6.023 × 1023) = 1.313 × 106 J of energy
4. But the 'energy required to remove the electron from one mole of atoms' is ionization enthalpy
■ So we can write:
The ionization enthalpy of atomic hydrogen in terms of J/mol is 1.313 × 106 J/mol
Solved example 3.13
Among the second period elements the actual ionization enthalpies are in the order Li < B < Be < C < O < N < F < Ne.
Explain why
(i) Be has higher ∆H than B
(ii) O has lower ∆H than N and F?
Solution:
Part (i):
See steps (10) to (12) above
Part (ii):
See steps (15) and (16) above
Solved example 3.14
How would you explain the fact that the first ionization enthalpy of sodium is lower than that of magnesium but its second ionization enthalpy is higher than that of magnesium?
Solution:
1. Let us write the electronic configurations:
• The electronic configuration of Na is [1s22s22p6]3s1
• The electronic configuration of Mg is [1s22s22p6]3s2
2. In both cases, the first electron will be removed from the 3s orbital
• The Mg has greater number of protons
• So it's electrons will be held more tightly
• Consequently, it's ΔH value will be higher than that of Na
3. Once the first electrons are removed,
• The electronic configuration of Na+ will be [1s22s22p6]
• The electronic configuration of Mg+ will be [1s22s22p6]3s1
4. We see that,
• In Na+, there is no third main-shell
♦ The configuration is same as that of the noble gas Ne
♦ It is very difficult to remove an electron from a noble gas configuration
• In Mg+, the last electron is present in the third main-shell
♦ That electron can be removed easily to attain noble gas configuration
5. That means,
• In Na+, the last electron is more tightly held to the nucleus than in Mg+
• So the second ionization enthalpy of Na will be higher than the second ionization enthalpy of Mg
Solved example 3.15
What are the various factors due to which the ionization enthalpy of the main group elements tends to decrease down a group?
Solution:
We can write 2 factors:
1. Increasing number of main-shells. This can be explained in 4 steps:
(i) When we move down the group, the number of main-shells increases
(ii) So the valence electrons are not tightly held to the nucleus
(iii) As a result, the valence electrons can be easily removed from the atom
(iv) In other words, the ΔH values become lower and lower
2. Increasing shielding effect. This can be explained in 6 steps:
(i) When we move down the group, the number of main-shells increases
(ii) So the number of inner shells also increases as we go down the group
(iii) This increases the shielding effect
• That is., when we move down the group, the valence electrons are more effectively shielded from the nucleus
(iv) So the valence electrons are not tightly held to the nucleus
(v) As a result, the valence electrons can be easily removed from the atom
(vi) In other words, the ΔH values become lower and lower
In the next section, we will see electron gain enthalpy
No comments:
Post a Comment