In the previous section 2.12, we saw dual nature of matter and uncertainty principle. We also saw the reasons for the failure of the Bohr model. In this section we will see the quantum mechanical model of the atom
■ We must first understand the difference between two branches of science:
(i) Classical mechanics
(ii) Quantum mechanics
We will write the details in steps:
1. Classical mechanics is based on Newton’s laws of motion (some notes can be seen here)
2. In classical mechanics, we can easily describe the motion of macroscopic objects. Let us see some examples:
• Consider a stone dropped from a height
♦ We can calculate the time required by the stone to reach the ground
♦ We can calculate the velocity with which the stone hits the ground
♦ We can calculate the position of the stone after any time interval ‘t’ after it is dropped
• Consider a car moving with an acceleration ‘a’
♦ We can calculate the time required by the car to reach the destination
♦ We can calculate the velocity of the car at any instant
♦ We can calculate the position of the car after any time interval ‘t’ since the beginning of the journey
3. But when we apply the principles of classical mechanics to microscopic particles like electrons, atoms, molecules etc., the ‘results obtained’ do not agree with the ‘experimental results’
4. The failure of classical mechanics in such cases is due to two reasons:
(i) Classical mechanics does not take into account, the wave nature of particles
• In the previous section, we saw that, microscopic particles exhibit significant wave nature
• So if we ignore the wave nature, the results will be all wrong
(ii) Classical mechanics does not take into account the uncertainty principle
• In the previous section, we saw that, uncertainty in position and velocity becomes significant in the case of microscopic particles
• So if we ignore the uncertainty, the results will be all wrong
5. In quantum mechanics, we take into account, both dual nature of matter and the uncertainty principle
6. We know that classical mechanics has it’s own laws related to the motion of objects
• Likewise, Quantum mechanics also has it’s own laws
• Laws which are related to the motion of particles
■ It is interesting to know this:
(i) We can apply the laws of classical mechanics to a macroscopic object
(ii) We can apply the laws of quantum mechanics to that same macroscopic object
• The results in (ii) will be same as the results in (i)
• Quantum mechanics was developed independently in 1926 by German scientist Warner Heisenberg and Austrian scientist Erwin Schrodinger
• Let us see how quantum mechanics help us to obtain the structure of the atom. We will write it in steps:
1. To get a clear picture about the structure of atom, we must know the ‘location of the electrons’ inside the atom
• We have seen that, laws of classical mechanics does not help us to locate the electrons
2. Schrodinger applied the laws of quantum mechanics and developed an 'equation'
• When this equation is solved, we get a set
• Each electron in an atom will have such a set
• The set of any one electron will be different from the set of other electrons
• In other words, the set is unique for each electron
3. What does each set contain?
• Answer: Each set contains four numbers
5. What is the significance of the four numbers?
• Answer:
♦ These four numbers are called quantum numbers
♦ The four numbers together will give the location of the electron
6. No two electrons can occupy the same location
■ So no two electrons will have the same set
7. But one important point is to be noted:
• According to Heisenberg’s uncertainty principle, we cannot determine both location and velocity with the same degree of accuracy
• So the ‘set of four quantum numbers’ does not give us the exact location
• They give us only a probability
• This can be explained using an example:
♦ A person is present inside a building
♦ The exact location of that person in the building is not known
♦ He could be any where in that building
• In the same manner, the ‘set of four quantum numbers’ gives us the location of a region
♦ The electron having that set could be anywhere in that region
• In the case of the person, the building is what is important
• In the case of the electron, the region is what is important
8. So four numbers give the address of an electron
• This is similar to the address of a person
9. Let us first see how the address of a person is specified
• In the fig.2.34(a) below, the yellow squares denote houses
• The thick red lines denote ‘main roads’
• We see that:
♦ Rows 1, 4, 5 and 8 have access to main-roads
• We see that:
♦ Rows 2, 3, 6 and 7 do not have access to any road
♦ There is no way to reach those houses
• Main roads have a greater width. They are expensive to make. It is not practical to provide more main-roads
• So we provide sub-roads
• In fig.b, sub-roads are shown in green color. They have a lesser width than main-roads
• Now we can reach any house
• The ‘address of any person in the locality’ will have four items as shown below:
♦ Name of person
♦ Name of house
♦ Name of sub-road
♦ Name of main-road
10. Two or more individuals in the locality may have the same name. But their house names will be different. Even if the house names are also same, the road names will be different So no two persons will have the same address. There will not be any confusion for the post man to deliver letters
• We can write:
♦ Each individual in a locality has a unique address
♦ Each electron in an atom also has a unique address
• The following steps will help us to understand how it is done
1. To reach a person, the postman reads upwards from the bottom most line. That is:
• First, he looks for the name of the main-road
• Then he looks for the name of the sub-road
• so on . . .
2. In the same way, we will work upwards from the bottom
(i) In a locality, we have main-roads
• In an atom, we have main-shells
♦ These main-shells can be distinguished from one another
♦ Because, each one of them have a unique number
(ii) The numbers possessed by the main shells are called principal quantum numbers
• The main-shell which is closest to the nucleus has the principal quantum number 1
• The next main-shell has the principal quantum number 2
• The main-shell coming after that, has the principal quantum number 3
• so on . . .
(iv) Principal quantum numbers are denoted by the letter n. So we can write:
• ‘n = 1’ indicates the main-shell closest to the nucleus
• ‘n = 2’ indicates the next main-shell
• ‘n = 3’ indicates the main-shell coming after that
• so on . . .
(v) We can say this:
When n increases, the distance from the nucleus increases
(vi) Letters are also used to represent main shells:
• Main-shell with n = 1 is represented using the letter K
• Main-shell with n = 2 is represented using the letter L
• Main-shell with n = 3 is represented using the letter M
• Main-shell with n = 4 is represented using the letter N
• so on . . .
3. We can prepare a table showing the comparison between the two items:
(i) Address of a person in a locality
(ii) Address of an electron in an atom
• Such a table is shown in fig.2.35 below:
• As we proceed in our discussion, we will get more and more information so as to fill up the blanks
4. Once the correct main-road is reached, the postman will look for the sub-roads
• Similarly, in the case of electrons, once the main-shell is reached, we look for sub-shells
• How many sub-shells are there?
• The answer can be written in steps:
♦ If we are at n = 1, we will see only 1 sub-shell
♦ If we are at n = 2, we will see 2 sub-shells
♦ If we are at n = 3, we will see 3 sub-shells
♦ If we are at n = 4, we will see 4 sub-shells
♦ so on . . .
• So we can write:
The number of sub-shells available in a main-shell is equal to the 'value of n of that main-shell'
5. Thus we see that, there can be many sub-shells
♦ These sub-shells can be distinguished from one another
♦ Because, each one of them have a unique number
• The numbers possessed by sub-shells are called azimuthal quantum numbers
♦ Azimuthal quantum numbers are also called orbital angular momentum quantum numbers
♦ Azimuthal quantum numbers are also called subsidiary quantum numbers
• Azimuthal quantum numbers are denoted by the letter ‘l’
6. We want to know how this l is assigned to each sub-shell. We can write it in steps:
(i) Assume that, we are at the main-shell with n = 1
• We see only one sub-shell
• That sub-shell will have the value: l = 0
(ii) Assume that, we are at the main-shell with n = 2
• We see two sub-shells
• The first one of those two sub-shells will have the value: l = 0
• The second one of those two sub-shells will have the value: l = 1
(iii) Assume that, we are at the main-shell with n = 3
• We see three sub-shells
• The first one of those three sub-shells will have the value: l = 0
• The second one of those three sub-shells will have the value: l = 1
• The third one of those three sub-shells will have the value: l = 2
(iv) Assume that, we are at the main-shell with n = 4
• We see four sub-shells
• The first one of those four sub-shells will have the value: l = 0
• The second one of those four sub-shells will have the value: l = 1
• The third one of those four sub-shells will have the value: l = 2
• The fourth one of those four sub-shells will have the value: l = 3
(v) Assume that, we are at the main-shell with n = 5
• We see five sub-shells
• The first one of those five sub-shells will have the value: l = 0
• The second one of those five sub-shells will have the value: l = 1
• The third one of those five sub-shells will have the value: l = 2
• The fourth one of those five sub-shells will have the value: l = 3
• The fifth one of those five sub-shells will have the value: l = 4
7. We see an interesting aspect here:
• The subshells with the same l value occur in more than one main-shells
For example:
The subshell with (l = 3) is present in the fourth and fifth main-shells
• This occurs in the case of roads also
An example:
The sub-road with (number = 2) will occur in many main-roads
8. However in our present case, the repetition follows a pattern:
• The sub-shell with (l = 0) occurs in all main-shells
• The sub-shell with (l = 1) occurs in all main-shells except (n=1)
• The sub-shell with (l = 2) occurs in all main-shells except (n=1) and (n= 2)
• The sub-shell with (l = 3) occurs in all main-shells except (n=1), (n=2) and (n= 3)
• so on . . .
9. We can write a general rule for assigning l value to sub-shells:
(i) Go to any main-shell
(ii) Write down the n value of that main-shell
(iii) There will be n sub-shells in that main-shell
♦ The first of those n sub-shells will have the value (l = 0)
♦ The second of those n sub-shells will have the value (l = 1)
♦ The third of those n sub-shells will have the value (l = 2)
♦ The fourth of those n sub-shells will have the value (l = 3)
♦ so on . . .
10. We saw that, the main-shells can be represented using both numbers and letters:
(n=1) is K, (n=2) is L, (n=3) is L so on . . .
• In a similar way, the sub-shells can also be represented using both numbers and letters:
(i) The sub-shells with (l=0) are represented using the letter s
• We call those sub-shells as : The s sub-shells
(ii) The sub-shells with (l=1) are represented using the letter p
• We call those sub-shells as : The p sub-shells
(iii) The sub-shells with (l=2) are represented using the letter d
• We call those sub-shells as : The d sub-shells
(iv) The sub-shells with (l=3) are represented using the letter f
• We call those sub-shells as : The f sub-shells
11. So we have seen sub-shells. We can add this information to the table that we prepared above in fig.2.35. The modified table is shown in fig.2.36 below:
• As we proceed in our discussion, we will get more and more information so as to fill up the remaining blanks also
12. In the sub-roads, there are houses
• So once the correct sub-road is reached, the postman will start looking for the correct house
• In our case, we have reached the sub-shells
• What do we see?
The answer can be written in steps:
(i) We see some regions
• These regions are not planar regions. They are 3-dimensional regions
♦ Planar regions have surface area only
♦ 3-dimensional regions have both surface area and volume
• Some of them have very peculiar shapes
(ii) We can count and see how many regions there are
• Also, we can give a description about their shapes
13. Consider the first sub-shell s. It’s quantum number is: (l = 0)
• In an atom, there will be:
♦ Only one main-shell K
♦ Only one main-shell L
♦ Only one main-shell M
♦ so on . . .
• But in that same atom, there will be:
♦ Many s sub-shells
♦ Many p sub-shells
♦ Many d sub-shells
♦ so on . . .
• We have already seen the reason for this in step (7). We must always keep this aspect in our minds
■ Assume that, we are at any one of the s sub-shells. It’s quantum number is: (l = 0)
♦ We will see only one region
♦ That region is spherical in shape
♦ The nucleus of the atom is present at the center of that sphere
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all s sub-shells will have only one region
14. Consider the second sub-shell p. It’s quantum number is: (l = 1)
■ Assume that, we are at any one of the many p sub-shells available
♦ We will see 3 regions
♦ All the 3 regions have the same shape. The shape of a dumbbell
• That means, we will see 3 dumbbells
• The shape of one of those 3 regions is shown in fig.2.37(a) below:
■ If all the three regions are of the same shape, how can we distinguish them from one another?
Answer can be written in steps:
(i) Though they have the same shape, they are oriented in different directions
• They are mutually perpendicular to each other
(ii) Since they are mutually perpendicular to each other, we can make use of our familiar ‘coordinate axes’
• One dumbbell lies along the x-axis. This is shown in the fig.2.37(b)
♦ It is given the name: $\mathbf\small{p_x}$
• Another dumbbell lies along the y-axis. This is shown in the fig.2.37(c)
♦ It is given the name: $\mathbf\small{p_y}$
• The third dumbbell lies along the z-axis. This is shown in the fig.2.37(d)
♦ It is given the name: $\mathbf\small{p_z}$
(iii) The 3 dumbbells do not have independent existence
• They are always seen together. This is shown in the fig.2.37(e)
(iv) In fig.e, the nucleus of the atom will be present at the center
♦ 'center' means, the 'point of intersection' of the 3 axes
• Note that, the 'lobes' of the dumbbells are distributed uniformly around the nucleus
• In the fig.e, however, the nucleus is hidden from the view because of the presence of the 'lobes' all around
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all p sub-shells will have only three regions
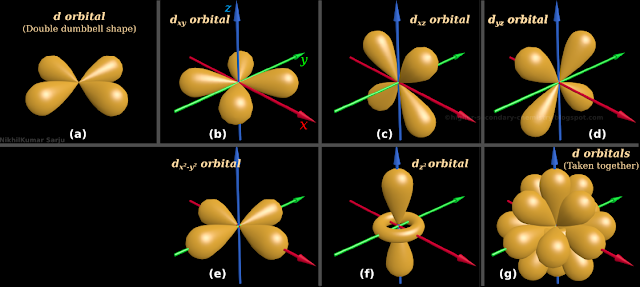
15. Consider the third sub-shell d. It’s quantum number is: (l = 2)
■ Assume that, we are at any one of those d sub-shells
♦ We will see 5 regions
♦ Four of those five regions have the same shape. The shape of a double dumbbell. It is shown in fig.2.38(a) below
• We must pay special attention here:
♦ The region shown in fig.a, is not a single dumbbell. It is a double dumbbell
♦ 'One whole double dumbbell' is one region
♦ There are four such regions
• The fifth region has a different shape. It is shown in fig.2.38(f)
• Consider the four similar shaped regions. How will we distinguish them from one another?
Answer can be written in steps:
(i) Though they have the same shape, they are oriented in different directions
So we will name them depending on the orientation
(ii) The first one lies in the xy-plane. This is shown in fig.2.38(b) above
♦ It is given the name: $\mathbf\small{d_{xy}}$
♦ We can imagine a 'plane which contains both x and y axes'
♦ The $\mathbf\small{d_{xy}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{xy}}$ are oriented along any particular axis
• The second one lies in the xz-plane. This is shown in fig.2.38(c) above
♦ It is given the name: $\mathbf\small{d_{xz}}$
♦ We can imagine a 'plane which contains both x and z axes'
♦ The $\mathbf\small{d_{xz}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{xz}}$ are oriented along any particular axis
• The third one lies in the yz-plane. This is shown in fig.2.38(d) above
♦ It is given the name: $\mathbf\small{d_{yz}}$
♦ We can imagine a 'plane which contains both y and z axes'
♦ The $\mathbf\small{d_{yz}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{yz}}$ are oriented along any particular axis
• The fourth one also has a double dumbbell shape
♦ One of the dumbbells lies along the x-axis
♦ The other dumbbell lies along the y-axis. This is shown in fig.2.38(e) above
♦ It is given the name: $\mathbf\small{d_{x^2-y^2}}$
• The fifth one lies along the z-axis
♦ It is a single dumbbell
♦ Also it has a circular region at the center. This is shown in fig.2.38(f) above
♦ It is given the name $\mathbf\small{d_{z^2}}$
(iii) The 5 regions do not have independent existence
• They are always seen together. This is shown in the fig.2.38(g)
• The circular portion $\mathbf\small{d_{z^2}}$ of is hidden from view. This is because, it has only a small radius
(iv) In fig.g, the nucleus of the atom will be present at the center
♦ 'center' means, the 'point of intersection' of the 3 axes
• Note that, the 'lobes' of the dumbbells are distributed uniformly around the nucleus
• In the fig.g, however, the nucleus is hidden from the view because of the presence of the 'lobes' all around
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all sub-shells coming third (the d sub-shells) have only five regions
16. Consider the fourth sub-shell f. It’s quantum number is: (l = 3)
■ Assume that, we are at any one of those f sub-shells
♦ We will see 7 regions
• Those 7 regions have very complicated shapes. At present we do not have to learn about those shapes. Also, we do not have to learn about their names. We will see those details in higher classes. All we need to remember now is that, in any f sub-shell, there will be 7 regions
17. Let us write a summary about the 'number of regions' in the various sub-shells:
♦ The s sub-shell (l=0) has 1 region
♦ The p sub-shell (l=1) has 3 regions
♦ The d sub-shell (l=2) has 5 regions
♦ The p sub-shell (l=3) has 7 regions
18. The official name of 'region' is orbital
• So we can write:
♦ The s sub-shell (l=0) has 1 orbital
♦ The p sub-shell (l=1) has 3 orbitals
♦ The d sub-shell (l=2) has 5 orbitals
♦ The p sub-shell (l=3) has 7 orbitals
19. Now we will see the numbers possessed by each of the orbitals
• We have seen these:
♦ Each of the main-shells possess a unique principal quantum number (n)
♦ Each of the sub-shells possess a unique azimuthal quantum number (l)
• In the same way:
♦ Each of the orbitals possess a unique magnetic orbital quantum number
♦ They are denoted by: ml
20. Let us see them in detail:
♦ The one and only orbital in the s sub-shell is given the ml number: 0
♦ The 3 orbitals in the p sub-shell are given the ml numbers: -1, 0, 1
♦ The 5 orbitals in the d sub-shell are given the ml numbers: -2, -1, 0, 1, 2
♦ The 7 orbitals in the f sub-shell are given the ml numbers: -3, -2, -1, 0, 1, 2, 3
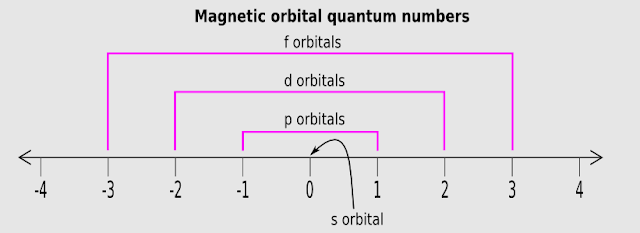
21. Let us see the method of assigning ml numbers. We will write it in steps:
(i) Consider any sub-shell
(ii) Write down the 'l' value of that sub-shell
(iii) Calculate (2l+1)
(iv) There will be a total of (2l+1) orbitals in that sub-shell
(v) Mark -l on the number line (see fig.2.39 below)
(vi) Mark l on the number line
(vii) Write down all the integers starting from -l and ending at l
(Only integers are allowed. We must not write down decimal values)
(viii) These integers are the ml values of the orbitals in that sub-shell
22. Let us apply these steps to the various orbitals:
The s sub-shell
(i) Consider the s sub-shell
(ii) It's l value is 0
(iii) (2l+1) = (2×0 + 1) = 1
(iv) So there will be only one orbital in the s sub-shell
(v) -l = -0 = 0
(vi) l = 0
(vii) There is only one integer to write: 0
(viii) There is only one orbital in the s sub-shell and it's ml value is 0
The p sub-shell
(i) Consider the p sub-shell
(ii) It's l value is 1
(iii) (2l+1) = (2×1 + 1) = 3
(iv) So there will be 3 orbitals in the p sub-shell
(v) -l = -1
(vi) l = 1
(vii) There are three integers to write: -1, 0, 1
(viii) There are three orbitals in the p sub-shell and their ml values are: -1, 0, 1
The d sub-shell
(i) Consider the d sub-shell
(ii) It's l value is 2
(iii) (2l+1) = (2×2 + 1) = 5
(iv) So there will be 5 orbitals in the d sub-shell
(v) -l = -2
(vi) l = 2
(vii) There are five integers to write: -2, -1, 0, 1, 2
(viii) There are five orbitals in the p sub-shell and their ml values are: -2, -1, 0, 1, 2
The f sub-shell
(i) Consider the f sub-shell
(ii) It's l value is 3
(iii) (2l+1) = (2×3 + 1) = 7
(iv) So there will be 7 orbitals in the d sub-shell
(v) -l = -3
(vi) l = 3
(vii) There are seven integers to write: -3, -2, -1, 0, 1, 2, 3
(viii) There are seven orbitals in the f sub-shell and their ml values are: -3, -2, -1, 0, 1, 2, 3
23. So we have seen orbitals. We can add this information to the table. The modified table is shown in fig.2.40 below:
• Note:
♦ In the above table, only the quantum numbers of s and p orbitals are shown
♦ We can make the list longer by adding d and f orbitals also
• As we proceed in our discussion, we will get more and more information so as to fill up the remaining blank also
■ We must first understand the difference between two branches of science:
(i) Classical mechanics
(ii) Quantum mechanics
We will write the details in steps:
1. Classical mechanics is based on Newton’s laws of motion (some notes can be seen here)
2. In classical mechanics, we can easily describe the motion of macroscopic objects. Let us see some examples:
• Consider a stone dropped from a height
♦ We can calculate the time required by the stone to reach the ground
♦ We can calculate the velocity with which the stone hits the ground
♦ We can calculate the position of the stone after any time interval ‘t’ after it is dropped
• Consider a car moving with an acceleration ‘a’
♦ We can calculate the time required by the car to reach the destination
♦ We can calculate the velocity of the car at any instant
♦ We can calculate the position of the car after any time interval ‘t’ since the beginning of the journey
3. But when we apply the principles of classical mechanics to microscopic particles like electrons, atoms, molecules etc., the ‘results obtained’ do not agree with the ‘experimental results’
4. The failure of classical mechanics in such cases is due to two reasons:
(i) Classical mechanics does not take into account, the wave nature of particles
• In the previous section, we saw that, microscopic particles exhibit significant wave nature
• So if we ignore the wave nature, the results will be all wrong
(ii) Classical mechanics does not take into account the uncertainty principle
• In the previous section, we saw that, uncertainty in position and velocity becomes significant in the case of microscopic particles
• So if we ignore the uncertainty, the results will be all wrong
5. In quantum mechanics, we take into account, both dual nature of matter and the uncertainty principle
6. We know that classical mechanics has it’s own laws related to the motion of objects
• Likewise, Quantum mechanics also has it’s own laws
• Laws which are related to the motion of particles
■ It is interesting to know this:
(i) We can apply the laws of classical mechanics to a macroscopic object
(ii) We can apply the laws of quantum mechanics to that same macroscopic object
• The results in (ii) will be same as the results in (i)
• Now we know the difference between classical mechanics and quantum mechanics
• Let us see how quantum mechanics help us to obtain the structure of the atom. We will write it in steps:
1. To get a clear picture about the structure of atom, we must know the ‘location of the electrons’ inside the atom
• We have seen that, laws of classical mechanics does not help us to locate the electrons
2. Schrodinger applied the laws of quantum mechanics and developed an 'equation'
• When this equation is solved, we get a set
• Each electron in an atom will have such a set
• The set of any one electron will be different from the set of other electrons
• In other words, the set is unique for each electron
3. What does each set contain?
• Answer: Each set contains four numbers
5. What is the significance of the four numbers?
• Answer:
♦ These four numbers are called quantum numbers
♦ The four numbers together will give the location of the electron
6. No two electrons can occupy the same location
■ So no two electrons will have the same set
7. But one important point is to be noted:
• According to Heisenberg’s uncertainty principle, we cannot determine both location and velocity with the same degree of accuracy
• So the ‘set of four quantum numbers’ does not give us the exact location
• They give us only a probability
• This can be explained using an example:
♦ A person is present inside a building
♦ The exact location of that person in the building is not known
♦ He could be any where in that building
• In the same manner, the ‘set of four quantum numbers’ gives us the location of a region
♦ The electron having that set could be anywhere in that region
• In the case of the person, the building is what is important
• In the case of the electron, the region is what is important
8. So four numbers give the address of an electron
• This is similar to the address of a person
9. Let us first see how the address of a person is specified
• In the fig.2.34(a) below, the yellow squares denote houses
• The thick red lines denote ‘main roads’
 |
| Fig.2.34 |
♦ Rows 1, 4, 5 and 8 have access to main-roads
• We see that:
♦ Rows 2, 3, 6 and 7 do not have access to any road
♦ There is no way to reach those houses
• Main roads have a greater width. They are expensive to make. It is not practical to provide more main-roads
• So we provide sub-roads
• In fig.b, sub-roads are shown in green color. They have a lesser width than main-roads
• Now we can reach any house
• The ‘address of any person in the locality’ will have four items as shown below:
♦ Name of person
♦ Name of house
♦ Name of sub-road
♦ Name of main-road
10. Two or more individuals in the locality may have the same name. But their house names will be different. Even if the house names are also same, the road names will be different So no two persons will have the same address. There will not be any confusion for the post man to deliver letters
• We can write:
♦ Each individual in a locality has a unique address
♦ Each electron in an atom also has a unique address
• The four quantum numbers help us to establish the address of each electron
1. To reach a person, the postman reads upwards from the bottom most line. That is:
• First, he looks for the name of the main-road
• Then he looks for the name of the sub-road
• so on . . .
2. In the same way, we will work upwards from the bottom
(i) In a locality, we have main-roads
• In an atom, we have main-shells
♦ These main-shells can be distinguished from one another
♦ Because, each one of them have a unique number
(ii) The numbers possessed by the main shells are called principal quantum numbers
• The main-shell which is closest to the nucleus has the principal quantum number 1
• The next main-shell has the principal quantum number 2
• The main-shell coming after that, has the principal quantum number 3
• so on . . .
(iv) Principal quantum numbers are denoted by the letter n. So we can write:
• ‘n = 1’ indicates the main-shell closest to the nucleus
• ‘n = 2’ indicates the next main-shell
• ‘n = 3’ indicates the main-shell coming after that
• so on . . .
(v) We can say this:
When n increases, the distance from the nucleus increases
(vi) Letters are also used to represent main shells:
• Main-shell with n = 1 is represented using the letter K
• Main-shell with n = 2 is represented using the letter L
• Main-shell with n = 3 is represented using the letter M
• Main-shell with n = 4 is represented using the letter N
• so on . . .
3. We can prepare a table showing the comparison between the two items:
(i) Address of a person in a locality
(ii) Address of an electron in an atom
• Such a table is shown in fig.2.35 below:
 |
| Fig.2.35 |
4. Once the correct main-road is reached, the postman will look for the sub-roads
• Similarly, in the case of electrons, once the main-shell is reached, we look for sub-shells
• How many sub-shells are there?
• The answer can be written in steps:
♦ If we are at n = 1, we will see only 1 sub-shell
♦ If we are at n = 2, we will see 2 sub-shells
♦ If we are at n = 3, we will see 3 sub-shells
♦ If we are at n = 4, we will see 4 sub-shells
♦ so on . . .
• So we can write:
The number of sub-shells available in a main-shell is equal to the 'value of n of that main-shell'
5. Thus we see that, there can be many sub-shells
♦ These sub-shells can be distinguished from one another
♦ Because, each one of them have a unique number
• The numbers possessed by sub-shells are called azimuthal quantum numbers
♦ Azimuthal quantum numbers are also called orbital angular momentum quantum numbers
♦ Azimuthal quantum numbers are also called subsidiary quantum numbers
• Azimuthal quantum numbers are denoted by the letter ‘l’
6. We want to know how this l is assigned to each sub-shell. We can write it in steps:
(i) Assume that, we are at the main-shell with n = 1
• We see only one sub-shell
• That sub-shell will have the value: l = 0
(ii) Assume that, we are at the main-shell with n = 2
• We see two sub-shells
• The first one of those two sub-shells will have the value: l = 0
• The second one of those two sub-shells will have the value: l = 1
(iii) Assume that, we are at the main-shell with n = 3
• We see three sub-shells
• The first one of those three sub-shells will have the value: l = 0
• The second one of those three sub-shells will have the value: l = 1
• The third one of those three sub-shells will have the value: l = 2
(iv) Assume that, we are at the main-shell with n = 4
• We see four sub-shells
• The first one of those four sub-shells will have the value: l = 0
• The second one of those four sub-shells will have the value: l = 1
• The third one of those four sub-shells will have the value: l = 2
• The fourth one of those four sub-shells will have the value: l = 3
(v) Assume that, we are at the main-shell with n = 5
• We see five sub-shells
• The first one of those five sub-shells will have the value: l = 0
• The second one of those five sub-shells will have the value: l = 1
• The third one of those five sub-shells will have the value: l = 2
• The fourth one of those five sub-shells will have the value: l = 3
• The fifth one of those five sub-shells will have the value: l = 4
7. We see an interesting aspect here:
• The subshells with the same l value occur in more than one main-shells
For example:
The subshell with (l = 3) is present in the fourth and fifth main-shells
• This occurs in the case of roads also
An example:
The sub-road with (number = 2) will occur in many main-roads
8. However in our present case, the repetition follows a pattern:
• The sub-shell with (l = 0) occurs in all main-shells
• The sub-shell with (l = 1) occurs in all main-shells except (n=1)
• The sub-shell with (l = 2) occurs in all main-shells except (n=1) and (n= 2)
• The sub-shell with (l = 3) occurs in all main-shells except (n=1), (n=2) and (n= 3)
• so on . . .
9. We can write a general rule for assigning l value to sub-shells:
(i) Go to any main-shell
(ii) Write down the n value of that main-shell
(iii) There will be n sub-shells in that main-shell
♦ The first of those n sub-shells will have the value (l = 0)
♦ The second of those n sub-shells will have the value (l = 1)
♦ The third of those n sub-shells will have the value (l = 2)
♦ The fourth of those n sub-shells will have the value (l = 3)
♦ so on . . .
10. We saw that, the main-shells can be represented using both numbers and letters:
(n=1) is K, (n=2) is L, (n=3) is L so on . . .
• In a similar way, the sub-shells can also be represented using both numbers and letters:
(i) The sub-shells with (l=0) are represented using the letter s
• We call those sub-shells as : The s sub-shells
(ii) The sub-shells with (l=1) are represented using the letter p
• We call those sub-shells as : The p sub-shells
(iii) The sub-shells with (l=2) are represented using the letter d
• We call those sub-shells as : The d sub-shells
(iv) The sub-shells with (l=3) are represented using the letter f
• We call those sub-shells as : The f sub-shells
11. So we have seen sub-shells. We can add this information to the table that we prepared above in fig.2.35. The modified table is shown in fig.2.36 below:
 |
| Fig.2.36 |
12. In the sub-roads, there are houses
• So once the correct sub-road is reached, the postman will start looking for the correct house
• In our case, we have reached the sub-shells
• What do we see?
The answer can be written in steps:
(i) We see some regions
• These regions are not planar regions. They are 3-dimensional regions
♦ Planar regions have surface area only
♦ 3-dimensional regions have both surface area and volume
• Some of them have very peculiar shapes
(ii) We can count and see how many regions there are
• Also, we can give a description about their shapes
13. Consider the first sub-shell s. It’s quantum number is: (l = 0)
• In an atom, there will be:
♦ Only one main-shell K
♦ Only one main-shell L
♦ Only one main-shell M
♦ so on . . .
• But in that same atom, there will be:
♦ Many s sub-shells
♦ Many p sub-shells
♦ Many d sub-shells
♦ so on . . .
• We have already seen the reason for this in step (7). We must always keep this aspect in our minds
■ Assume that, we are at any one of the s sub-shells. It’s quantum number is: (l = 0)
♦ We will see only one region
♦ That region is spherical in shape
♦ The nucleus of the atom is present at the center of that sphere
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all s sub-shells will have only one region
14. Consider the second sub-shell p. It’s quantum number is: (l = 1)
■ Assume that, we are at any one of the many p sub-shells available
♦ We will see 3 regions
♦ All the 3 regions have the same shape. The shape of a dumbbell
• That means, we will see 3 dumbbells
• The shape of one of those 3 regions is shown in fig.2.37(a) below:
 |
| Fig.2.37 |
Answer can be written in steps:
(i) Though they have the same shape, they are oriented in different directions
• They are mutually perpendicular to each other
(ii) Since they are mutually perpendicular to each other, we can make use of our familiar ‘coordinate axes’
• One dumbbell lies along the x-axis. This is shown in the fig.2.37(b)
♦ It is given the name: $\mathbf\small{p_x}$
• Another dumbbell lies along the y-axis. This is shown in the fig.2.37(c)
♦ It is given the name: $\mathbf\small{p_y}$
• The third dumbbell lies along the z-axis. This is shown in the fig.2.37(d)
♦ It is given the name: $\mathbf\small{p_z}$
(iii) The 3 dumbbells do not have independent existence
• They are always seen together. This is shown in the fig.2.37(e)
(iv) In fig.e, the nucleus of the atom will be present at the center
♦ 'center' means, the 'point of intersection' of the 3 axes
• Note that, the 'lobes' of the dumbbells are distributed uniformly around the nucleus
• In the fig.e, however, the nucleus is hidden from the view because of the presence of the 'lobes' all around
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all p sub-shells will have only three regions
15. Consider the third sub-shell d. It’s quantum number is: (l = 2)
■ Assume that, we are at any one of those d sub-shells
♦ We will see 5 regions
♦ Four of those five regions have the same shape. The shape of a double dumbbell. It is shown in fig.2.38(a) below
• We must pay special attention here:
♦ The region shown in fig.a, is not a single dumbbell. It is a double dumbbell
♦ 'One whole double dumbbell' is one region
♦ There are four such regions
• The fifth region has a different shape. It is shown in fig.2.38(f)
 |
| Fig.2.38 |
Answer can be written in steps:
(i) Though they have the same shape, they are oriented in different directions
So we will name them depending on the orientation
(ii) The first one lies in the xy-plane. This is shown in fig.2.38(b) above
♦ It is given the name: $\mathbf\small{d_{xy}}$
♦ We can imagine a 'plane which contains both x and y axes'
♦ The $\mathbf\small{d_{xy}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{xy}}$ are oriented along any particular axis
• The second one lies in the xz-plane. This is shown in fig.2.38(c) above
♦ It is given the name: $\mathbf\small{d_{xz}}$
♦ We can imagine a 'plane which contains both x and z axes'
♦ The $\mathbf\small{d_{xz}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{xz}}$ are oriented along any particular axis
• The third one lies in the yz-plane. This is shown in fig.2.38(d) above
♦ It is given the name: $\mathbf\small{d_{yz}}$
♦ We can imagine a 'plane which contains both y and z axes'
♦ The $\mathbf\small{d_{yz}}$ region lies exactly in that plane
♦ Note that, none of the dumbbells of $\mathbf\small{d_{yz}}$ are oriented along any particular axis
• The fourth one also has a double dumbbell shape
♦ One of the dumbbells lies along the x-axis
♦ The other dumbbell lies along the y-axis. This is shown in fig.2.38(e) above
♦ It is given the name: $\mathbf\small{d_{x^2-y^2}}$
• The fifth one lies along the z-axis
♦ It is a single dumbbell
♦ Also it has a circular region at the center. This is shown in fig.2.38(f) above
♦ It is given the name $\mathbf\small{d_{z^2}}$
(iii) The 5 regions do not have independent existence
• They are always seen together. This is shown in the fig.2.38(g)
• The circular portion $\mathbf\small{d_{z^2}}$ of is hidden from view. This is because, it has only a small radius
(iv) In fig.g, the nucleus of the atom will be present at the center
♦ 'center' means, the 'point of intersection' of the 3 axes
• Note that, the 'lobes' of the dumbbells are distributed uniformly around the nucleus
• In the fig.g, however, the nucleus is hidden from the view because of the presence of the 'lobes' all around
■ We can write a comparison:
♦ In a locality, any sub-road can have any number of houses
♦ In an atom, all sub-shells coming third (the d sub-shells) have only five regions
16. Consider the fourth sub-shell f. It’s quantum number is: (l = 3)
■ Assume that, we are at any one of those f sub-shells
♦ We will see 7 regions
• Those 7 regions have very complicated shapes. At present we do not have to learn about those shapes. Also, we do not have to learn about their names. We will see those details in higher classes. All we need to remember now is that, in any f sub-shell, there will be 7 regions
17. Let us write a summary about the 'number of regions' in the various sub-shells:
♦ The s sub-shell (l=0) has 1 region
♦ The p sub-shell (l=1) has 3 regions
♦ The d sub-shell (l=2) has 5 regions
♦ The p sub-shell (l=3) has 7 regions
18. The official name of 'region' is orbital
• So we can write:
♦ The s sub-shell (l=0) has 1 orbital
♦ The p sub-shell (l=1) has 3 orbitals
♦ The d sub-shell (l=2) has 5 orbitals
♦ The p sub-shell (l=3) has 7 orbitals
19. Now we will see the numbers possessed by each of the orbitals
• We have seen these:
♦ Each of the main-shells possess a unique principal quantum number (n)
♦ Each of the sub-shells possess a unique azimuthal quantum number (l)
• In the same way:
♦ Each of the orbitals possess a unique magnetic orbital quantum number
♦ They are denoted by: ml
20. Let us see them in detail:
♦ The one and only orbital in the s sub-shell is given the ml number: 0
♦ The 3 orbitals in the p sub-shell are given the ml numbers: -1, 0, 1
♦ The 5 orbitals in the d sub-shell are given the ml numbers: -2, -1, 0, 1, 2
♦ The 7 orbitals in the f sub-shell are given the ml numbers: -3, -2, -1, 0, 1, 2, 3
21. Let us see the method of assigning ml numbers. We will write it in steps:
(i) Consider any sub-shell
(ii) Write down the 'l' value of that sub-shell
(iii) Calculate (2l+1)
(iv) There will be a total of (2l+1) orbitals in that sub-shell
(v) Mark -l on the number line (see fig.2.39 below)
(vi) Mark l on the number line
(vii) Write down all the integers starting from -l and ending at l
(Only integers are allowed. We must not write down decimal values)
(viii) These integers are the ml values of the orbitals in that sub-shell
 |
| Fig.2.39 |
The s sub-shell
(i) Consider the s sub-shell
(ii) It's l value is 0
(iii) (2l+1) = (2×0 + 1) = 1
(iv) So there will be only one orbital in the s sub-shell
(v) -l = -0 = 0
(vi) l = 0
(vii) There is only one integer to write: 0
(viii) There is only one orbital in the s sub-shell and it's ml value is 0
The p sub-shell
(i) Consider the p sub-shell
(ii) It's l value is 1
(iii) (2l+1) = (2×1 + 1) = 3
(iv) So there will be 3 orbitals in the p sub-shell
(v) -l = -1
(vi) l = 1
(vii) There are three integers to write: -1, 0, 1
(viii) There are three orbitals in the p sub-shell and their ml values are: -1, 0, 1
The d sub-shell
(i) Consider the d sub-shell
(ii) It's l value is 2
(iii) (2l+1) = (2×2 + 1) = 5
(iv) So there will be 5 orbitals in the d sub-shell
(v) -l = -2
(vi) l = 2
(vii) There are five integers to write: -2, -1, 0, 1, 2
(viii) There are five orbitals in the p sub-shell and their ml values are: -2, -1, 0, 1, 2
The f sub-shell
(i) Consider the f sub-shell
(ii) It's l value is 3
(iii) (2l+1) = (2×3 + 1) = 7
(iv) So there will be 7 orbitals in the d sub-shell
(v) -l = -3
(vi) l = 3
(vii) There are seven integers to write: -3, -2, -1, 0, 1, 2, 3
(viii) There are seven orbitals in the f sub-shell and their ml values are: -3, -2, -1, 0, 1, 2, 3
23. So we have seen orbitals. We can add this information to the table. The modified table is shown in fig.2.40 below:
 |
| Fig.2.40 |
♦ In the above table, only the quantum numbers of s and p orbitals are shown
♦ We can make the list longer by adding d and f orbitals also
• As we proceed in our discussion, we will get more and more information so as to fill up the remaining blank also
We have written 23 steps. We will see the remaining steps in the next section
No comments:
Post a Comment